题目内容
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
.
(1)记动点P的轨迹为曲线D.求曲线D的方程,并说明方程表示的曲线;
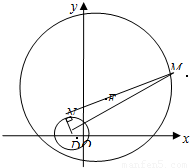
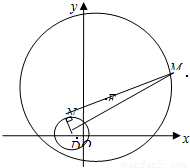
(2)若M是圆E:(x-2)2+(y-4)2=64上任意一点,过M作曲线D的切线,切点是N,求|MN|的取值范围.
| 1 | 2 |
(1)记动点P的轨迹为曲线D.求曲线D的方程,并说明方程表示的曲线;
(2)若M是圆E:(x-2)2+(y-4)2=64上任意一点,过M作曲线D的切线,切点是N,求|MN|的取值范围.
分析:(1)设动点P的坐标为(x,y),则由2|PO|=|PA|,由两点间的距离公式即可得出;
(2)先判断两圆的位置关系.由|MN|2=|MD|2-|DN|2,可得|MN|2=|MD|2-4,又|MD|min=8-5=3,|MD|max=8+5=13,即可得出.
(2)先判断两圆的位置关系.由|MN|2=|MD|2-|DN|2,可得|MN|2=|MD|2-4,又|MD|min=8-5=3,|MD|max=8+5=13,即可得出.
解答:解(1)设动点P的坐标为(x,y),则由2|PO|=|PA|,得4(x2+y2)=(x-3)2+y2,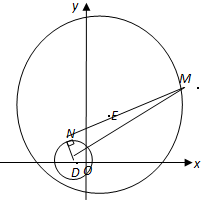
整理得:x2+y2+2x-3=0.
化为(x+1)2+y2=4,
因此曲线D的方程表示的是以(-1,0)为圆心,2为半径的圆.
(Ⅱ)由|DE|=
=5,及5<8-2有:两圆内含,且圆D在圆E内部.
如图所示,由|MN|2=|MD|2-|DN|2,即:|MN|2=|MD|2-4,
∵|MD|min=8-5=3,|MD|max=8+5=13,
故5≤|MN|2≤165,

整理得:x2+y2+2x-3=0.
化为(x+1)2+y2=4,
因此曲线D的方程表示的是以(-1,0)为圆心,2为半径的圆.
(Ⅱ)由|DE|=
| (2+1)2+(4-0)2 |
如图所示,由|MN|2=|MD|2-|DN|2,即:|MN|2=|MD|2-4,
∵|MD|min=8-5=3,|MD|max=8+5=13,
故5≤|MN|2≤165,
点评:本题考查了圆的标准方程及其性质、直线与圆的位置关系、切线的性质、勾股定理、最值问题的转化等基础知识与基本技能方法,属于难题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是
已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是 (2007•深圳一模)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足
(2007•深圳一模)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足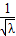 .
.
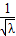 .
.