题目内容

当0＜a＜1时，在同一坐标系中，函数y=a^-x与y=log_ax的图象是（　　）

A、

B、

C、

D、

分析：先将函数y=a^-x化成指数函数的形式，再结合函数的单调性同时考虑这两个函数的单调性即可判断出结果

解答：解：∵函数y=a^-x与可化为
函数y=(

1

a

)x，其底数大于1，是增函数，
又y=log_ax，当0＜a＜1时是减函数，
两个函数是一增一减，前增后减．
故选C．

点评：本题考查函数的图象，考查同学们对对数函数和指数函数基础知识的把握程度以及数形结合的思维能力．

练习册系列答案

小学英语测试AB卷系列答案

学法大视野单元测试卷系列答案

新领程必考口算应用题系列答案

教材全析系列答案

全优学练测随堂学案系列答案

优加口算题卡系列答案

节节高名师课时计划系列答案

举一反三奥数1000题全解系列答案

全品高分小练习系列答案

达标加提高测试卷系列答案

相关题目

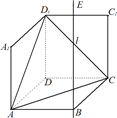如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A₁和CD D′C₁都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D₁．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D₁位于平面ABCD同侧（图2）．
（Ⅰ）设二面角E-AC-D₁的大小为θ，若

，求线段BE长的取值范围；
（Ⅱ）在线段D₁E上存在点P，使平面PA₁C₁∥平面EAC，求

与BE之间满足的关系式，并证明：当0＜BE＜a时，恒有

（2013•绵阳二模）设m是一个正整数，对两个正整数a、b，若a-b=km（k∈Z，k≠0），我们称a、b模m同余，用符号a=b（Modm）表示；在6=b（Modm）中，当

∈N，且m＞1时，b的所有可取值为

设m是一个正整数，对两个正整数a、b，若a-b=km（k∈Z，k≠0），我们称a、b模m同余，用符号a=b（Modm）表示；在6=b（Modm）中，当 $数学公式$ ，且m＞1时，b的所有可取值为________．

设m是一个正整数，对两个正整数a、b，若a-b=km（k∈Z，k≠0），我们称a、b模m同余，用符号a=b（Modm）表示；在6=b（Modm）中，当

，且m＞1时，b的所有可取值为．

设m是一个正整数，对两个正整数a、b，若a-b=km（k∈Z，k≠0），我们称a、b模m同余，用符号a=b（Modm）表示；在6=b（Modm）中，当

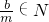，且m＞1时，b的所有可取值为．