题目内容
关于二次函数f(x)=x2+(m-1)x+1
(1)若?x∈R,f(x)>0恒成立,求实数m的取值范围;
(2)若方程f(x)=0在区间[0,2]上有解,求实数m的取值范围.
解:(1)∵?x∈R,f(x)>0恒成立,
∴△=(m-1)2-4<0
∴m2-2m-3<0
解得-1<m,3…(5分)
(2)∵f(x)=0在区间[0,2]上有解,又f(0)=1≠0
∴f(x)=0在区间(0,2]上有解
由x2+(m-1)x+1=0得m=1-(x+ )…(8分)
)…(8分)
当0<x≤2时,x+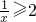 由(1)m≤1-2=-1
由(1)m≤1-2=-1
因此实数m的取值范围是:(-∞,-1]…(12分)
分析:(1)由题意可得△=(m-1)2-4<0,解不等式可求
(2)由f(0)=1≠0可知f(x)=0在区间(0,2]上有解,由x2+(m-1)x+1=0得m=1-(x+ ),结合基本不等式可求m的范围
),结合基本不等式可求m的范围
点评:本题主要考查了二次函数的恒成立与基本不等式在函数的最值求解中的应用,解题的关键是熟练掌握基本知识
∴△=(m-1)2-4<0
∴m2-2m-3<0
解得-1<m,3…(5分)
(2)∵f(x)=0在区间[0,2]上有解,又f(0)=1≠0
∴f(x)=0在区间(0,2]上有解
由x2+(m-1)x+1=0得m=1-(x+
 )…(8分)
)…(8分)当0<x≤2时,x+
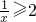 由(1)m≤1-2=-1
由(1)m≤1-2=-1因此实数m的取值范围是:(-∞,-1]…(12分)
分析:(1)由题意可得△=(m-1)2-4<0,解不等式可求
(2)由f(0)=1≠0可知f(x)=0在区间(0,2]上有解,由x2+(m-1)x+1=0得m=1-(x+
 ),结合基本不等式可求m的范围
),结合基本不等式可求m的范围点评:本题主要考查了二次函数的恒成立与基本不等式在函数的最值求解中的应用,解题的关键是熟练掌握基本知识

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目