题目内容
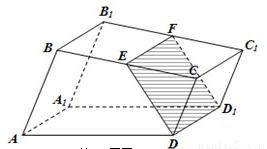
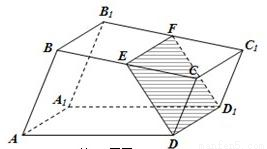
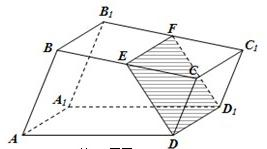 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.(Ⅰ)证明:无论点E怎样运动,四边形EFD1D都为矩形;
(Ⅱ)当EC=1时,求几何体A-EFD1D的体积.
分析:(I)要证明无论点E怎样运动,四边形EFD1D都为矩形,我们可根据已知中直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,先由线面平行的性质定理,判断出四边形EFD1D为平行四边形,再证明其邻边相互垂直,进而得到答案.
(II)连接AE,我们易根据已知条件,结合直棱柱的几何特征和勾股定理,判断出AE到为四棱锥的高,根据CD=DD1=1,AB=2,BC=3及EC=1,我们计算出四棱锥底面面积的和高,代入棱锥体积公式即可得到答案.
(II)连接AE,我们易根据已知条件,结合直棱柱的几何特征和勾股定理,判断出AE到为四棱锥的高,根据CD=DD1=1,AB=2,BC=3及EC=1,我们计算出四棱锥底面面积的和高,代入棱锥体积公式即可得到答案.
解答: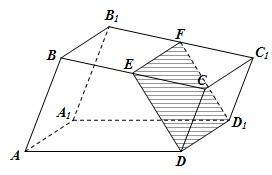 解:(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,DD1∥CC1,
解:(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,DD1∥CC1,
∵EF∥CC1,∴EF∥DD1,(2分)
又∵平面ABCD∥平面A1B1C1D1,
平面ABCD∩平面EFD1D=ED,
平面A1B1C1D1∩平面EFD1D=FD1,
∴ED∥FD1,∴四边形EFD1D为平行四边形,(4分)
∵侧棱DD1⊥底面ABCD,又DE?平面ABCD内,
∴DD1⊥DE,∴四边形EFD1D为矩形;(5分)
(Ⅱ)证明:连接AE,∵四棱柱ABCD-A1B1C1D1为直四棱柱,
∴侧棱DD1⊥底面ABCD,又AE?平面ABCD内,
∴DD1⊥AE,(6分)
在Rt△ABE中,AB=2,BE=2,则AE=2
;(7分)
在Rt△CDE中,EC=1,CD=1,则DE=
;(8分)
在直角梯形中ABCD,AD=
=
;
∴AE2+DE2=AD2,即AE⊥ED,
又∵ED∩DD1=D,∴AE⊥平面EFD1D;(10分)
由(Ⅰ)可知,四边形EFD1D为矩形,且DE=
,DD1=1,
∴矩形EFD1D的面积为SEFD1D=DE•DD1=
,
∴几何体A-EFD1D的体积为VA-EFD1D=
SEFD1D•AE=
×
×2
=
.
 解:(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,DD1∥CC1,
解:(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,DD1∥CC1,∵EF∥CC1,∴EF∥DD1,(2分)
又∵平面ABCD∥平面A1B1C1D1,
平面ABCD∩平面EFD1D=ED,
平面A1B1C1D1∩平面EFD1D=FD1,
∴ED∥FD1,∴四边形EFD1D为平行四边形,(4分)
∵侧棱DD1⊥底面ABCD,又DE?平面ABCD内,
∴DD1⊥DE,∴四边形EFD1D为矩形;(5分)
(Ⅱ)证明:连接AE,∵四棱柱ABCD-A1B1C1D1为直四棱柱,
∴侧棱DD1⊥底面ABCD,又AE?平面ABCD内,
∴DD1⊥AE,(6分)
在Rt△ABE中,AB=2,BE=2,则AE=2
| 2 |
在Rt△CDE中,EC=1,CD=1,则DE=
| 2 |
在直角梯形中ABCD,AD=
| BC2+(AB-CD)2 |
| 10 |
∴AE2+DE2=AD2,即AE⊥ED,
又∵ED∩DD1=D,∴AE⊥平面EFD1D;(10分)
由(Ⅰ)可知,四边形EFD1D为矩形,且DE=
| 2 |
∴矩形EFD1D的面积为SEFD1D=DE•DD1=
| 2 |
∴几何体A-EFD1D的体积为VA-EFD1D=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
| 4 |
| 3 |
点评:本题考查的知识点是棱锥的体积公式及平面的基本性质及推论,其中求几何体A-EFD1D的体积,关键是要找到棱锥的高,求出高和底面面积后,代入棱锥体积公式即可得到答案.

练习册系列答案
相关题目
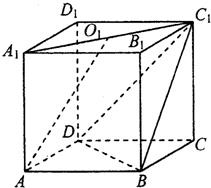 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点. 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: