题目内容
向一个边长为 的正三角形内随机投一点P,则点P到三边的距离都不小于1的概率为
的正三角形内随机投一点P,则点P到三边的距离都不小于1的概率为
- A.

- B.

- C.

- D.

C
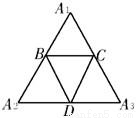
分析:在正三角形的内侧作三条平行线分别与三边平行,且距离等于1,可得到个小正三角形,可知落在小正三角形区域的点满足条件,所求概率即为小正三角形面积与大正三角形面积之比.
解答:在正三角形的内侧作三条平行线分别与三边平行,且距离等于1,可得到个小正三角形,可知落在小正三角形区域的点满足条件,所求概率即为小正三角形面积与大正三角形面积之比
∵大正三角形的边长为4 ,
,
∴大正三角形高为6,小正三角形高3,相似比为1:2,
∴两个三角形的面积比为 =
= .
.
故选C.
点评:本题考查几何概型,考查学生的计算能力,属于基础题.
分析:在正三角形的内侧作三条平行线分别与三边平行,且距离等于1,可得到个小正三角形,可知落在小正三角形区域的点满足条件,所求概率即为小正三角形面积与大正三角形面积之比.
解答:在正三角形的内侧作三条平行线分别与三边平行,且距离等于1,可得到个小正三角形,可知落在小正三角形区域的点满足条件,所求概率即为小正三角形面积与大正三角形面积之比
∵大正三角形的边长为4
 ,
,∴大正三角形高为6,小正三角形高3,相似比为1:2,
∴两个三角形的面积比为
 =
= .
.故选C.
点评:本题考查几何概型,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
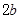 的正
的正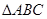 内接于椭圆
内接于椭圆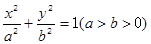 ,顶点
,顶点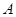 的坐标为
的坐标为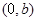 ,且高在
,且高在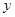 轴上,则椭圆的离心率为__________.
轴上,则椭圆的离心率为__________.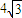 的正三角形内随机投一点P,则点P到三边的距离都不小于1的概率为( )
的正三角形内随机投一点P,则点P到三边的距离都不小于1的概率为( )



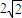 的正三角形(如图所示),则该三棱锥的外接球的表面积是 .
的正三角形(如图所示),则该三棱锥的外接球的表面积是 .