题目内容
(如图)p1为边长为1的正三角形纸板,在p1的左下端剪去一个边长为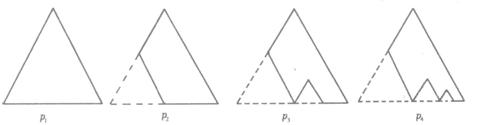
![]()
解析:本题考查了等比数列及极限的相关知识.由题意,第一个三角形的边长为1,剪去的第二个三角形的边长为![]() ,……,剪去的第n个三角形的边长an=
,……,剪去的第n个三角形的边长an=![]() ,边长为a的三角形的面积为S=
,边长为a的三角形的面积为S=![]() ×a×
×a×![]() a=
a=![]() a2.所以剪去的n个三角形面积之和为
a2.所以剪去的n个三角形面积之和为![]() (al2+a22+…+an2),数列{an2}是以a12=
(al2+a22+…+an2),数列{an2}是以a12=![]() 为首项q=
为首项q=![]() 为公比的等比数列.
为公比的等比数列.
Tn=![]() ×
×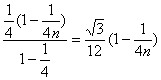 ,
,
所以Sn=![]() -
-![]()
![]()

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
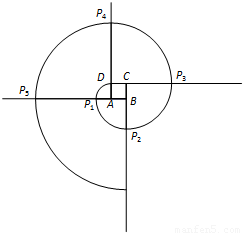
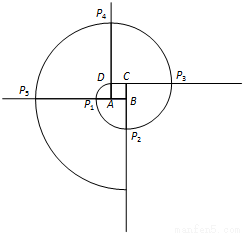
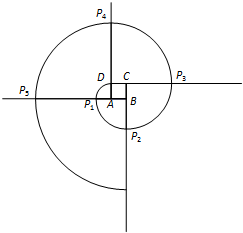 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是