题目内容
函数f(x)=2sinπx与函数g(x)=
的图象所有交点的橫坐标之和为______.
| 3 | x-1 |
函数g(x)=
关于(1,0)对称,函数g(x)单调递增,
且函数f(x)=2sinπx也关于(1,0)对称,
由
=2,解得x-1=8,即x=9,
由
=-2,解得x-1=-8,即x=-7,
∴两个函数f(x)和g(x)共有17个交点,除(1,0)外,其他16个交点关于(1,0)对称,
设对称的两个点的横坐标分别为a,b,
则
=1,即a+b=2,
∴函数f(x)=2sinπx与函数g(x)=
的图象所有交点的橫坐标之和为:
8(a+b)+1=8×2+1=17.
故答案为:17.
| 3 | x-1 |

且函数f(x)=2sinπx也关于(1,0)对称,
由
| 3 | x-1 |
由
| 3 | x-1 |
∴两个函数f(x)和g(x)共有17个交点,除(1,0)外,其他16个交点关于(1,0)对称,
设对称的两个点的横坐标分别为a,b,
则
| a+b |
| 2 |
∴函数f(x)=2sinπx与函数g(x)=
| 3 | x-1 |
8(a+b)+1=8×2+1=17.
故答案为:17.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
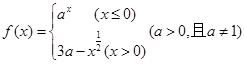 是
是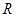 上的减函数,则
上的减函数,则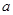 的取值范围是_____.
的取值范围是_____. ,则
,则 的值等于 .
的值等于 . ,若
,若 ,则a=
,则a=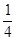

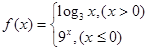 ,则
,则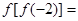 .
.