题目内容
已知抛物线 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)过点 作两相互垂直的弦
作两相互垂直的弦 ,设
,设 的横坐标为
的横坐标为 ,用
,用 表示△
表示△ 的面积,并求△
的面积,并求△ 面积的最小值;
面积的最小值;
(Ⅱ)过抛物线上一点 引圆
引圆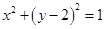 的两条切线
的两条切线 ,分别交抛物线于点
,分别交抛物线于点 , 连接
, 连接 ,求直线
,求直线 的斜率.
的斜率.
【答案】
(Ⅰ)当 时,△
时,△ 面积取得最小值1.
面积取得最小值1.
(Ⅱ)直线 的斜率为
的斜率为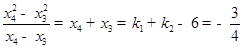 .
.
【解析】(I)先设 ,根据
,根据 得
得 .
.
因为  所以
所以 ,然后求出|OM|,|ON|的长,再利用面积公式求出面积S关于m的表达式,再利用求函数最值的方法求最值即可.
,然后求出|OM|,|ON|的长,再利用面积公式求出面积S关于m的表达式,再利用求函数最值的方法求最值即可.
(II) 设 ,直线AB的方程为
,直线AB的方程为 ,
,
AC的方程为 .因为 直线
.因为 直线 与圆
与圆 相切,
相切,
所以 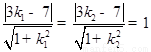 .,所以
.,所以  .
.
所以  是方程
是方程 的两根.(*)
的两根.(*)
然后由方程组 得
得 .
.
所以  ,同理可得:
,同理可得: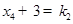 .
.
所以直线 的斜率为
的斜率为 .从而根据(*)和韦达定理即可求出BC的斜率值.
.从而根据(*)和韦达定理即可求出BC的斜率值.

练习册系列答案
相关题目
 ,
, 为坐标原点,动直线
为坐标原点,动直线 与
与 交于不同两点
交于不同两点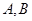
 ·
· 为常数;
为常数; 的点
的点 的轨迹方程。
的轨迹方程。