题目内容
2．函数y=${（\frac{1}{2}）}^{sin（-x）}$的单调递增区间是[2kπ-$\frac{π}{2}$，2kπ+$\frac{π}{2}$]，k∈z．分析 令t=sinx，则有y=2t，本题即求函数t的增区间．再利用正弦函数的图象可得函数t的增区间．
解答 解：令t=sinx，则有函数y=${（\frac{1}{2}）}^{sin（-x）}$=2sinx =2t，故本题即求函数t的增区间．
再利用正弦函数的图象可得函数t的增区间为[2kπ-$\frac{π}{2}$，2kπ+$\frac{π}{2}$]，
故答案为：[2kπ-$\frac{π}{2}$，2kπ+$\frac{π}{2}$]，k∈z．
点评 本题主要考查复合函数的单调性，指数函数的单调性，正弦函数的单调性，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
17．
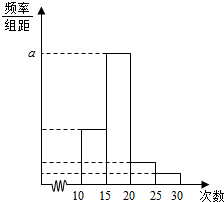对某校高一年级学生参加“社区志愿者”活动次数进行统计，随机抽取M名学生作为样本，得到这M个学生参加“社区志愿者”活动的次数．据此作出频数和频率统计表及频率分布直方图如下：
（Ⅰ）求出表中M，p及图中a的值；
（Ⅱ）若该校高一学生有720人，试估计他们参加“社区志愿者”活动的次数在[15，20）内的人数；
（Ⅲ）若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”，试估计小明被评为“优秀志愿者”的概率．
对某校高一年级学生参加“社区志愿者”活动次数进行统计，随机抽取M名学生作为样本，得到这M个学生参加“社区志愿者”活动的次数．据此作出频数和频率统计表及频率分布直方图如下：| 分组 | 频数 | 频率 |
| [10，15） | 5 | 0.25 |
| [15，20） | 12 | n |
| [20，25） | m | p |
| [25，30] | 1 | 0.05 |
| 合计 | M | 1 |
（Ⅱ）若该校高一学生有720人，试估计他们参加“社区志愿者”活动的次数在[15，20）内的人数；
（Ⅲ）若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”，试估计小明被评为“优秀志愿者”的概率．
已知斜四棱柱ABCD-A1B1C1D1的底面是矩形，侧面CC1D1D垂直底面ABCD，BC=2AB=DC1=2，BD1=2$\sqrt{3}$
12．设全集U=R，已知A=$\left\{{x\left|{\frac{2x+3}{x-2}＞0}\right.}\right\}$，B={x||x-1|＜2}，则（∁UA）∩B=（ ）
| A． | $（{-\frac{3}{2}，1}）$ | B． | （-1，2] | C． | （2，3] | D． | [2，3） |