题目内容
已知圆C经过坐标原点,且与直线x-y+2=0相切,切点为A(2,4).(1)求圆C的方程;
(2)若斜率为-1的直线l与圆C相交于不同的两点M,N,求
 的取值范围..
的取值范围..
【答案】分析:(1)解法一:求出直线AC的方程,再求出线段OA的垂直平分线方程,联立方程组求出圆心C的坐标,可得圆的半径,
从而写出C的方程.
解法二:设圆C的方程为(x-a)2+(y-b)2=r2,根据点A和点O在圆上,圆心到切线的距离等于半径建立方程组,
求出a、b、r的值 从而求出C的方程.
(2)解:设直线l的方程为y=x+m,M(x1,y1),N(x2,y2),把直线方程代入圆的方程利用根与系数的关系求出
x1+x2和x1•x2的值,代入 的解析式化简为(m-6)2.再根据圆心到直线的距离小于半径求出m的范围,即可得到(m-6)2的距离.
的解析式化简为(m-6)2.再根据圆心到直线的距离小于半径求出m的范围,即可得到(m-6)2的距离.
解答:(1)解法一:圆的圆心为C,依题意得直线AC的斜率KAC=-1,
∴直线AC的方程为y-4=-(x-2),即x+y-6=0.
∵直线OA的斜率KOA= =2,∴线段OA的垂直平分线为y-2=
=2,∴线段OA的垂直平分线为y-2= (x-1),即x+2y-5=0.
(x-1),即x+2y-5=0.
解方程组 得圆心C的坐标为(7,-1).
得圆心C的坐标为(7,-1).
∴圆C的半径为r=|AC|= =5
=5 ,
,
∴圆C的方程为(x-7)2+(y+1)2=50.
解法二:设圆C的方程为(x-a)2+(y-b)2=r2,
依题意得 ,解得
,解得  ,∴圆的方程为:(x-7)2+(y+1)2=50.
,∴圆的方程为:(x-7)2+(y+1)2=50.
(2)解:设直线l的方程为y=-x+m,M(x1,y1),N(x2,y2).
由 消去y得 2x2-(2m+16)x+m2+2m=0.
消去y得 2x2-(2m+16)x+m2+2m=0.
∴x1+x2=m+8, .
.
∴ =(x1-2)(x2-2)+(y1-4)(y2-4)
=(x1-2)(x2-2)+(y1-4)(y2-4)
=(x1-2)(x2-2)+(-x1+m-4)(-x2+m-4)=2x1•x2-(m-2)(x1+x2)+(m-4)2+4
=m2+2-(m-2)(m+8)+(m-4)2+4=m2-12m+36=(m-6)2.
∵直线l与圆C相交于不同两点,∴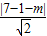 <5
<5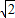 ,解得-4<m<16.
,解得-4<m<16.
∴0≤(m-6)2<100,
∴ 的取值范围是[0,100).
的取值范围是[0,100).
点评:本题主要考查两个向量数量积公式的应用,直线和圆的位置关系的应用,属于中档题.
从而写出C的方程.
解法二:设圆C的方程为(x-a)2+(y-b)2=r2,根据点A和点O在圆上,圆心到切线的距离等于半径建立方程组,
求出a、b、r的值 从而求出C的方程.
(2)解:设直线l的方程为y=x+m,M(x1,y1),N(x2,y2),把直线方程代入圆的方程利用根与系数的关系求出
x1+x2和x1•x2的值,代入
 的解析式化简为(m-6)2.再根据圆心到直线的距离小于半径求出m的范围,即可得到(m-6)2的距离.
的解析式化简为(m-6)2.再根据圆心到直线的距离小于半径求出m的范围,即可得到(m-6)2的距离.解答:(1)解法一:圆的圆心为C,依题意得直线AC的斜率KAC=-1,
∴直线AC的方程为y-4=-(x-2),即x+y-6=0.
∵直线OA的斜率KOA=
 =2,∴线段OA的垂直平分线为y-2=
=2,∴线段OA的垂直平分线为y-2= (x-1),即x+2y-5=0.
(x-1),即x+2y-5=0.解方程组
 得圆心C的坐标为(7,-1).
得圆心C的坐标为(7,-1).∴圆C的半径为r=|AC|=
 =5
=5 ,
,∴圆C的方程为(x-7)2+(y+1)2=50.
解法二:设圆C的方程为(x-a)2+(y-b)2=r2,
依题意得
 ,解得
,解得  ,∴圆的方程为:(x-7)2+(y+1)2=50.
,∴圆的方程为:(x-7)2+(y+1)2=50.(2)解:设直线l的方程为y=-x+m,M(x1,y1),N(x2,y2).
由
 消去y得 2x2-(2m+16)x+m2+2m=0.
消去y得 2x2-(2m+16)x+m2+2m=0.∴x1+x2=m+8,
 .
.∴
 =(x1-2)(x2-2)+(y1-4)(y2-4)
=(x1-2)(x2-2)+(y1-4)(y2-4)=(x1-2)(x2-2)+(-x1+m-4)(-x2+m-4)=2x1•x2-(m-2)(x1+x2)+(m-4)2+4
=m2+2-(m-2)(m+8)+(m-4)2+4=m2-12m+36=(m-6)2.
∵直线l与圆C相交于不同两点,∴
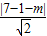 <5
<5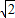 ,解得-4<m<16.
,解得-4<m<16.∴0≤(m-6)2<100,
∴
 的取值范围是[0,100).
的取值范围是[0,100).点评:本题主要考查两个向量数量积公式的应用,直线和圆的位置关系的应用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目