题目内容
已知椭圆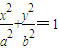 与双曲线
与双曲线 具有相同的焦点F1,F2,且顶点P(0,b)满足
具有相同的焦点F1,F2,且顶点P(0,b)满足 .
.(1)求椭圆的方程;
(2)设过抛物线x2=12y焦点F的直线交椭圆于A、B两点,若
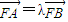 ,求实数λ的范围.
,求实数λ的范围.
【答案】分析:(1)由双曲线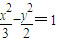 的焦点F1(-
的焦点F1(-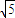 ,0),F2(
,0),F2(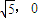 ),知椭圆
),知椭圆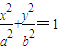 的焦点F1(-
的焦点F1(-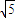 ,0),F2(
,0),F2(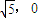 ),由此能求出椭圆的方程.
),由此能求出椭圆的方程.
(2)设直线AB的方程为y=kx+3,联立方程组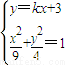 ,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由
,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由 ,知
,知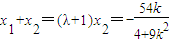 ,
,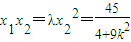 ,由此能求出实数λ的范围.
,由此能求出实数λ的范围.
解答:解:(1)∵双曲线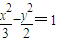 的焦点F1(-
的焦点F1(-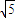 ,0),F2(
,0),F2(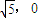 ),
),
∴椭圆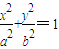 的焦点F1(-
的焦点F1(-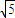 ,0),F2(
,0),F2(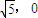 ),
),
∴a2-b2=5.
∵椭圆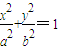 的顶点P(0,b)满足
的顶点P(0,b)满足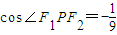 ,
,
∴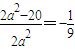 ,
,
解得a2=9,
∴b2=4,
故椭圆的方程为: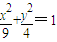 .
.
(2)设直线AB的方程为y=kx+3,
联立方程组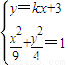 ,
,
得(4+9k2)x2+54kx+45=0,
设A(x1,y1),B(x2,y2),
∵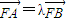 ,
,
∴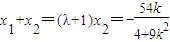 ,①
,①
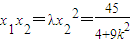 ,②
,②
由①得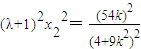 ,③
,③
③÷②,得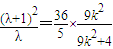 ,
,
∴ ,
,
整理,得5λ2-26λ+5≤0,
∴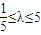 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
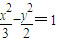 的焦点F1(-
的焦点F1(-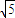 ,0),F2(
,0),F2(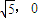 ),知椭圆
),知椭圆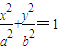 的焦点F1(-
的焦点F1(-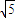 ,0),F2(
,0),F2(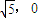 ),由此能求出椭圆的方程.
),由此能求出椭圆的方程.(2)设直线AB的方程为y=kx+3,联立方程组
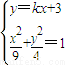 ,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由
,得(4+9k2)x2+54kx+45=0,设A(x1,y1),B(x2,y2),由 ,知
,知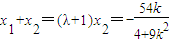 ,
,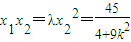 ,由此能求出实数λ的范围.
,由此能求出实数λ的范围.解答:解:(1)∵双曲线
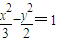 的焦点F1(-
的焦点F1(-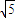 ,0),F2(
,0),F2(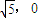 ),
),∴椭圆
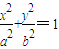 的焦点F1(-
的焦点F1(-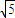 ,0),F2(
,0),F2(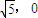 ),
),∴a2-b2=5.
∵椭圆
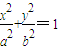 的顶点P(0,b)满足
的顶点P(0,b)满足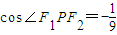 ,
,∴
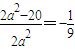 ,
,解得a2=9,
∴b2=4,
故椭圆的方程为:
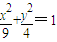 .
.(2)设直线AB的方程为y=kx+3,
联立方程组
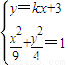 ,
,得(4+9k2)x2+54kx+45=0,
设A(x1,y1),B(x2,y2),
∵
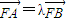 ,
,∴
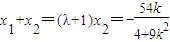 ,①
,①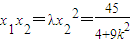 ,②
,②由①得
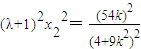 ,③
,③③÷②,得
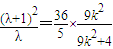 ,
,∴
 ,
,整理,得5λ2-26λ+5≤0,
∴
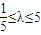 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
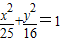 与双曲线
与双曲线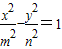 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 . 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 . 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .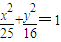 与双曲线
与双曲线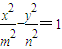 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .