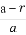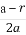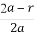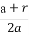题目内容
设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
(1)若随机数b,c∈{1,2,3,4}.
(2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b=4*Rand( )和c=4*Rand( )的执行结果.(注:符号“*”表示“乘号”)
(1) 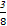 (2)
(2) 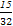
【解析】由f(x)=x2+bx+c知,事件A“f(1)≤5且f(0)≤3”,即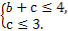
(1)因为随机数b,c∈{1,2,3,4},所以共等可能地产生16个数对(b,c),
列举如下:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),
(3,4),(4,1),(4,2),(4,3),(4,4).
事件A: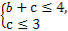 包含了其中6个数对(b,c),即:(1,1),
包含了其中6个数对(b,c),即:(1,1),
(1,2),(1,3),(2,1),(2,2),(3,1).
所以P(A)=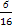 =
=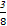 ,即事件A发生的概率为
,即事件A发生的概率为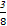 .
.
(2)由题意,b,c均是区间[0,4]中的随机数,产生的点(b,c)均匀地分布在边长为4的正方形区域Ω中(如图),其面积S(Ω)=16.
事件A: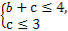 所对应的区域为如图所示的梯形(阴影部分),
所对应的区域为如图所示的梯形(阴影部分),
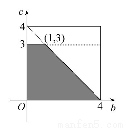
其面积为:S(A)=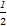 ×(1+4)×3=
×(1+4)×3=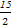 ,
,
所以P(A)=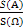 =
=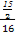 =
=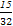 ,
,
即事件A发生的概率为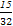 .
.

练习册系列答案
相关题目