题目内容
以下命题:①二直线平行的充要条件是它们的斜率相等;
②过圆上的点(x,y)与圆x2+y2=r2相切的直线方程是
 ;
;③平面内到两定点的距离之和等于常数的点的轨迹是椭圆;
④抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.
其中正确命题的标号是 .
【答案】分析:根据两条直线平行的充要条件知第一个命题不正确,根据圆的切线方程得到第二个正确.第三个命题不正确,若平面内到两定点距离之和等于常数,常数为大于两个点的距离;根据抛物线的定义对第四个命题进行判断即可.
解答:解:①两条直线平行的充要条件是它们的斜率相等,且截距不等,故①不正确,
②过点(x,y)与圆x2+y2=r2相切的直线方程是xx+yy=r2.②正确,
③不正确,若平面内到两定点距离之和等于常数,如这个常数正好为两个点的距离,则动点的轨迹是两点的连线段,而不是椭圆;
④根据抛物线的定义知:抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.故④正确.
故答案为:②④.
点评:本题考查命题真假的判断,考查了圆锥曲线的共同特征,同时考查了椭圆与双曲线的性质,本题解题的关键是对于所给的几个不同的知识点要正确理解,本题是一个基础题.
解答:解:①两条直线平行的充要条件是它们的斜率相等,且截距不等,故①不正确,
②过点(x,y)与圆x2+y2=r2相切的直线方程是xx+yy=r2.②正确,
③不正确,若平面内到两定点距离之和等于常数,如这个常数正好为两个点的距离,则动点的轨迹是两点的连线段,而不是椭圆;
④根据抛物线的定义知:抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.故④正确.
故答案为:②④.
点评:本题考查命题真假的判断,考查了圆锥曲线的共同特征,同时考查了椭圆与双曲线的性质,本题解题的关键是对于所给的几个不同的知识点要正确理解,本题是一个基础题.

练习册系列答案
相关题目
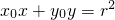 ;
;