题目内容
已知平面区域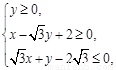 的外接圆
的外接圆 与
与 轴交于点
轴交于点 ,椭圆
,椭圆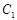 以线段
以线段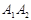
为长轴,离心率 .
.
(1)求圆 及椭圆
及椭圆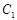 的方程;
的方程;
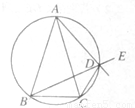
(2)设椭圆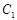 的右焦点为
的右焦点为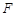 ,点
,点 为圆
为圆 上异于
上异于 的动点,过原点
的动点,过原点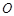 作直线
作直线 的垂线交直线
的垂线交直线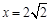 于点
于点 ,判断直线
,判断直线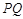 与圆
与圆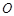 的位置关系,并给出证明。
的位置关系,并给出证明。
【答案】
 ,
,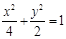
当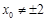 时,
时,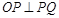 ,故直线PQ始终与圆C相切
,故直线PQ始终与圆C相切
【解析】解:(1)由题意可知,平面区域是以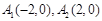 及点
及点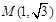 为顶点的三角形,
为顶点的三角形,
∵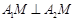 ,∴
,∴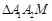 为直角三角形,∴外接圆
为直角三角形,∴外接圆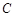 以原点
以原点 为圆心,
为圆心,
线段 为直径,故其方程为
为直径,故其方程为 .
……4分
.
……4分
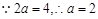 .又
.又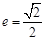 ,∴
,∴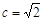 ,可得
,可得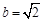 .
.
∴所求椭圆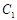 的方程是
的方程是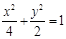 .
……………6分
.
……………6分
(2)直线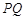 与圆
与圆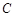 相切.设
相切.设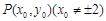 ,则
,则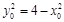 .
.
当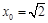 时,
时,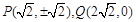 ,
,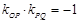 ,∴
,∴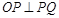 ; ……8分
; ……8分
当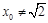 时,
时, ,∴
,∴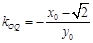 .
……9分
.
……9分
∴直线 的方程为
的方程为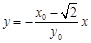 .因此,点
.因此,点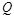 的坐标为
的坐标为 .∵
.∵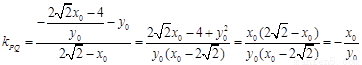 ,
,
∴当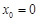 时,
时,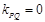 ,
,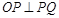 ;
;
当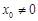 时候,
时候,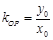 ,∴
,∴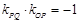 ,∴
,∴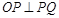 .
………12分[来
.
………12分[来
综上所述,当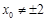 时,
时,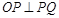 ,故直线PQ始终与圆C相切. ………13分
,故直线PQ始终与圆C相切. ………13分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.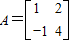
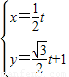 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.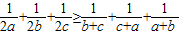 .
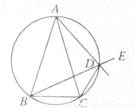
.
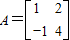
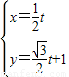 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.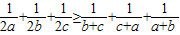 .
.

 (t为参数),求直线l被曲线C截得的线段长度.
(t为参数),求直线l被曲线C截得的线段长度.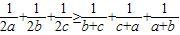 .
.