Question

7、设m、n为不重合的两条直线，α、β为不重合的两个平面，下列命题为真命题的是（　　）

A、如果m、n是异面直线，m?α，n?α，那么n∥α；

B、如果m、n是异面直线，m?α，n?α，那么n与α相交；

C、如果m、n共面，m?α，n∥α，那么m∥n；

D、如果m?β，m∥α，n?α，n∥β，那么m∥n

Answer 1

分析：对于答案A，n可以和平面α相交，故A错，
对于B，n可以和平面α平行，故B错，
对于C，因为m、n共面，所以m、n平行或相交，又m?α，n∥α，所以m∥n；即C对，
对于D，因为当α∥β时，m、n可能是异面直线，故D错．

解答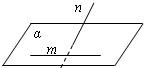：解：如图，可知（A）不正确
对于（B），当n与α平行时，也可以满足m与n异面的条件，故（B）不正确
对于（C），因为m、n共面，可设这个平面为γ，又因为m?α，故m是平面α与γ的交线
根据线面平行的性质定理，当n∥α时，必定有m∥n．（C）正确
对于（D），当α与β相交时命题正确，但当α∥β时，m、n可能是异面直线．故（D）错误
故选：C

点评：本题考查空间中直线和平面的位置关系．涉及到两直线共面和异面，线面平行等知识点，在证明线面平行时，其常用方法是在平面内找已知直线平行的直线．当然也可以用面面平行来推导线面平行．