题目内容
(文科做)已知函数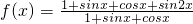
(1)求证: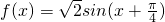 ;
;
(2)求函数y=f(x)的定义域.
证:(1)左边= =
= =右边.证毕.
=右边.证毕.
(2)x 需满足
,即 ,
,
∴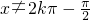 ,且x≠2kπ-π,(k∈Z).
,且x≠2kπ-π,(k∈Z).
∴函数的定义域为:
分析:(1)将分子中的1用sin2x+cos2x代替,利用二倍角公式将sin2x用2sinxcosx表示,利用完全平方公式,合并同类项,得证.
(2)令分母不为0,通过解三角不等式 ,求出x的范围,写成集合形式即为函数的定义域.
,求出x的范围,写成集合形式即为函数的定义域.
点评:本题考查三角函数中1的灵活运用,三角函数中二倍角的应用,是一道中档题.
 =
= =右边.证毕.
=右边.证毕.(2)x 需满足

,即
 ,
,∴
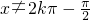 ,且x≠2kπ-π,(k∈Z).
,且x≠2kπ-π,(k∈Z).∴函数的定义域为:

分析:(1)将分子中的1用sin2x+cos2x代替,利用二倍角公式将sin2x用2sinxcosx表示,利用完全平方公式,合并同类项,得证.
(2)令分母不为0,通过解三角不等式
 ,求出x的范围,写成集合形式即为函数的定义域.
,求出x的范围,写成集合形式即为函数的定义域.点评:本题考查三角函数中1的灵活运用,三角函数中二倍角的应用,是一道中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
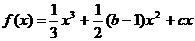 (b、c为常数).
(b、c为常数).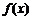 在
在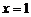 和
和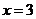 处取得极值,试求
处取得极值,试求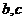 的值;
的值;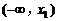 、
、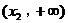 上单调递增,且在
上单调递增,且在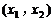 上单调递减,又满足
上单调递减,又满足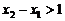 ,求证:
,求证: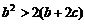 。
。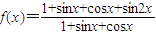
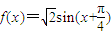 ;
;