题目内容
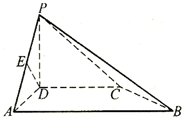
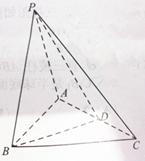
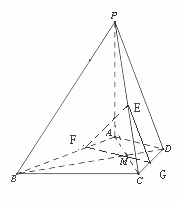
如图,在四棱锥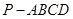 中,
中,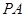 ⊥面
⊥面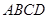 ,
,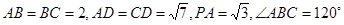
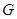 为线段
为线段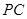 上的点.
上的点.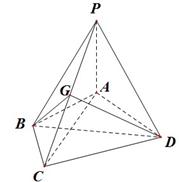
(Ⅰ)证明: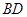 ⊥面
⊥面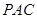 ;
;
(Ⅱ)若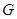 是
是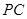 的中点,求
的中点,求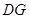 与
与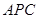 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若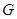 满足
满足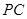 ⊥面
⊥面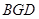 ,求
,求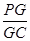 的值.
的值.
(Ⅰ)详见解析;(Ⅱ)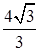 ;(Ⅲ)
;(Ⅲ)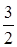
解析试题分析:(Ⅰ)证BD与面PAC内的两条相交线PA和AC都垂直,根据线面垂直可证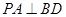 ,利用证角等于
,利用证角等于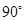 的方法可证
的方法可证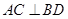 ,详见解析。(Ⅱ) 设
,详见解析。(Ⅱ) 设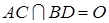 ,由(1)知
,由(1)知 ,所以GO为GD在面PAC内的摄影,所以
,所以GO为GD在面PAC内的摄影,所以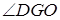 即为所求,在直角三角形中利用三角函数即可求出。(Ⅲ)根据(Ⅰ)中条件可求出
即为所求,在直角三角形中利用三角函数即可求出。(Ⅲ)根据(Ⅰ)中条件可求出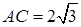 ,在直角三角形中利用勾股定理求出
,在直角三角形中利用勾股定理求出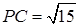 ,同理求出
,同理求出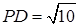 ,根据已知
,根据已知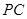 ⊥面
⊥面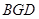 可得
可得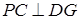 ,根据两直角三角形用公共边可列出方程求解。
,根据两直角三角形用公共边可列出方程求解。
试题解析:证明:(Ⅰ)由已知得三角形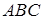 是等腰三角形,且底角等于30°,且
是等腰三角形,且底角等于30°,且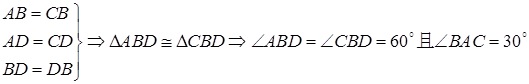 ,所以;、
,所以;、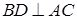 ,又因为
,又因为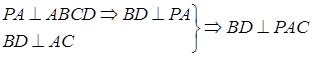 ;
;
(Ⅱ)设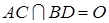 ,由(1)知
,由(1)知 ,连接
,连接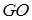 ,所以
,所以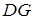 与面
与面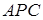 所成的角是
所成的角是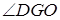 ,由已知及(1)知:
,由已知及(1)知: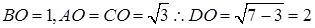 ,
, 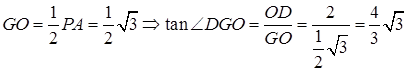 ,所以
,所以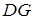 与面
与面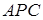 所成的角的正切值是
所成的角的正切值是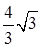 ;
;
(Ⅲ)由已知得到: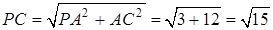 ,因为
,因为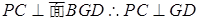 ,在
,在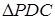 中,
中,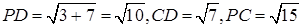 ,因为
,因为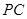 ⊥面
⊥面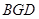 ,
,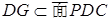 ,所以
,所以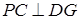 ,设
,设 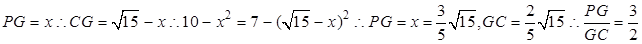
考点:线面垂直,线面角

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
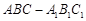 中,
中,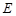 ,
,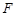 分别为
分别为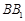 ,
,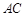 的中点.
的中点.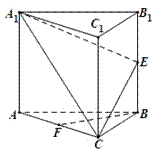
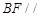 平面
平面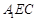 ;
;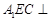 平面
平面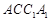 .
.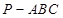 中,
中,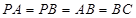 ,
,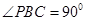 ,D为AC的中点,
,D为AC的中点,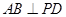 .
.
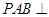 平面
平面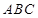 ;
;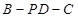 的余弦值.
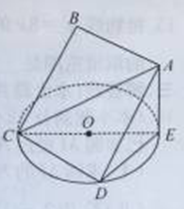
的余弦值.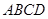 所在平面与圆
所在平面与圆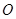 所在的平面相交于
所在的平面相交于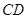 ,线段
,线段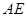 垂直于圆
垂直于圆 为圆
为圆 、
、 的点,设正方形
的点,设正方形 ,且
,且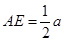 .
.
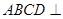 平面
平面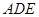 ;
;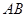 与
与 所成的角为
所成的角为 ,
,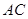 与底面
与底面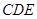 所成角为
所成角为 ,二面角
,二面角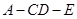 所成角为
所成角为 ,求证
,求证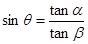
 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.
 中,已知平面
中,已知平面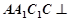 平面
平面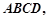 且
且 ,
, .
.

 为棱
为棱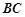 的中点,求证:
的中点,求证: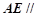 平面
平面 .
.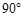 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.