题目内容
已知点A,B分别是射线l1:y=x(x≥0),l2:y=-x(x≥0)上的动点,O为坐标原点,且△OAB的面积为定值2.(I)求线段AB中点M的轨迹C的方程;
(II)过点N(0,2)作直线l,与曲线C交于不同的两点P,Q,与射线l1,l2分别交于点R,S,试求出直线l的斜率的取值范围,并证明:|PR|=|QS|.
【答案】分析:(1)设点M(x,y),由M是线段AB中点得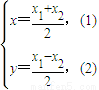 又因为点A,B分别是射线l1l2上的动点,且S△OAB=x1x2=2所以点M的轨迹方程为x2-y2=2(x>0).
又因为点A,B分别是射线l1l2上的动点,且S△OAB=x1x2=2所以点M的轨迹方程为x2-y2=2(x>0).
(Ⅱ)讨论直线的斜率是否存在,存在时设直线l的方程为y=kx+2,由题得xP,xQ>0,即整理得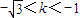 ,又
,又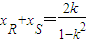 且PQ的中点的横坐标为
且PQ的中点的横坐标为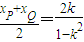 ,所以
,所以
|PR|=|QS|
解答:解:(I)由题可设A(x1,x1),B(x2,-x2),M(x,y),其中x1>0,x2>0.
则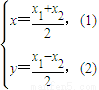
∵△OAB的面积为定值2,
∴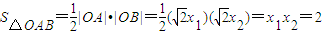 .
.
(1)2-(2)2,消去x1,x2,得:x2-y2=2.
由于x1>0,x2>0,∴x>0,所以点M的轨迹方程为x2-y2=2(x>0).
(II)依题意,直线l的斜率存在,设直线l的方程为y=kx+2.
由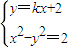 消去y得:(1-k2)x2-4kx-6=0,
消去y得:(1-k2)x2-4kx-6=0,
设点P、Q、R、S的横坐标分别是xP、xQ、xR、xP,
∴由xP,xQ>0得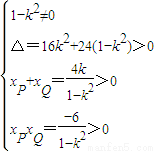
解之得: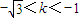
由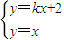 消去y得:
消去y得: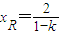 ,
,
由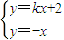 消去y得:
消去y得: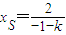
∴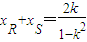 .又PQ的中点的横坐标为
.又PQ的中点的横坐标为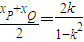
所以RS的中点与PQ的中点重合,故|PR|=|QS|
点评:本题主要考查双曲线轨迹方程以及弦的中点问题与直线和圆锥曲线的相交问题,它们是圆锥曲线的综合问题也是高考常考内容.
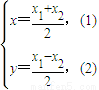 又因为点A,B分别是射线l1l2上的动点,且S△OAB=x1x2=2所以点M的轨迹方程为x2-y2=2(x>0).
又因为点A,B分别是射线l1l2上的动点,且S△OAB=x1x2=2所以点M的轨迹方程为x2-y2=2(x>0).(Ⅱ)讨论直线的斜率是否存在,存在时设直线l的方程为y=kx+2,由题得xP,xQ>0,即整理得
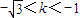 ,又
,又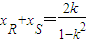 且PQ的中点的横坐标为
且PQ的中点的横坐标为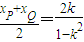 ,所以
,所以|PR|=|QS|
解答:解:(I)由题可设A(x1,x1),B(x2,-x2),M(x,y),其中x1>0,x2>0.
则
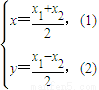
∵△OAB的面积为定值2,
∴
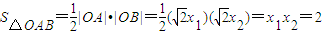 .
.(1)2-(2)2,消去x1,x2,得:x2-y2=2.
由于x1>0,x2>0,∴x>0,所以点M的轨迹方程为x2-y2=2(x>0).
(II)依题意,直线l的斜率存在,设直线l的方程为y=kx+2.
由
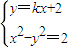 消去y得:(1-k2)x2-4kx-6=0,
消去y得:(1-k2)x2-4kx-6=0,设点P、Q、R、S的横坐标分别是xP、xQ、xR、xP,
∴由xP,xQ>0得
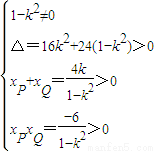
解之得:
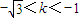
由
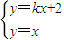 消去y得:
消去y得: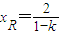 ,
,由
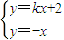 消去y得:
消去y得: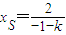
∴
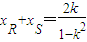 .又PQ的中点的横坐标为
.又PQ的中点的横坐标为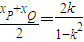
所以RS的中点与PQ的中点重合,故|PR|=|QS|
点评:本题主要考查双曲线轨迹方程以及弦的中点问题与直线和圆锥曲线的相交问题,它们是圆锥曲线的综合问题也是高考常考内容.

练习册系列答案
相关题目