题目内容
(2011•湖北)(1)已知函数f(x)=lnx﹣x+1,x∈(0,+∞),求函数f(x)的最大值;
(2)设a1,b1(k=1,2…,n)均为正数,证明:
①若a1b1+a2b2+…anbn≤b1+b2+…bn,则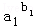
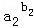 …
…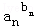 ≤1;
≤1;
②若b1+b2+…bn=1,则 ≤
≤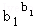
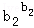 …
…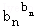 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.
(2)设a1,b1(k=1,2…,n)均为正数,证明:
①若a1b1+a2b2+…anbn≤b1+b2+…bn,则
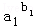
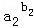 …
…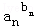 ≤1;
≤1;②若b1+b2+…bn=1,则
 ≤
≤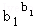
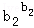 …
…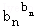 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.(1)0 (2)见解析
(1)f(x)的定义域为(0,+∞),
令f′(x)= ﹣1=0,解得x=1,
﹣1=0,解得x=1,
当0<x<1时,f′(x)>0,所以f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,所以f(x)在(1,+∞)上是减函数;
故函数f(x)在x=1处取得最大值f(1)=0;
(2)①由(1)知,当x∈(0,+∞)时,有f(x)≤f(1)=0,即lnx≤x﹣1,
∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak﹣1,
得bklnak≤akbk﹣bk(k=1,2…,n),
求和得

 ≤a1b1+a2b2+…+anbn﹣(b1+b2+…+bn)
≤a1b1+a2b2+…+anbn﹣(b1+b2+…+bn)
∵a1b1+a2b2+…anbn≤b1+b2+…bn,
∴

 ≤0,即ln
≤0,即ln ≤0,
≤0,
∴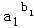
 …
… ≤1;
≤1;
②先证 ≤
≤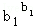
 …
… ,
,
令ak=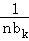 (k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
(k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
于是由①得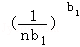
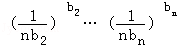 ≤1,即
≤1,即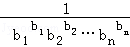 ≤nb1+b2+…bn=n,
≤nb1+b2+…bn=n,
∴ ≤
≤
 …
…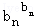 ,
,
②再证
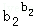 …
…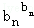 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,
记s=b12+b22+…+bn2.令ak= (k=1,2…,n),
(k=1,2…,n),
则a1b1+a2b2+…+anbn= (b12+b22+…+bn2)=1=b1+b2+…bn,
(b12+b22+…+bn2)=1=b1+b2+…bn,
于是由(1)得 ≤1,
≤1,
即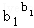
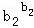 …
… ≤sb1+b2+…bn=s,
≤sb1+b2+…bn=s,
∴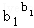
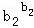 …
… ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,
综合①②,②得证.
令f′(x)=
 ﹣1=0,解得x=1,
﹣1=0,解得x=1,当0<x<1时,f′(x)>0,所以f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,所以f(x)在(1,+∞)上是减函数;
故函数f(x)在x=1处取得最大值f(1)=0;
(2)①由(1)知,当x∈(0,+∞)时,有f(x)≤f(1)=0,即lnx≤x﹣1,
∵ak,bk(k=1,2…,n)均为正数,从而有lnak≤ak﹣1,
得bklnak≤akbk﹣bk(k=1,2…,n),
求和得


 ≤a1b1+a2b2+…+anbn﹣(b1+b2+…+bn)
≤a1b1+a2b2+…+anbn﹣(b1+b2+…+bn)∵a1b1+a2b2+…anbn≤b1+b2+…bn,
∴


 ≤0,即ln
≤0,即ln ≤0,
≤0,∴
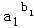
 …
… ≤1;
≤1;②先证
 ≤
≤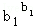
 …
… ,
,令ak=
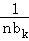 (k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,
(k=1,2…,n),则a1b1+a2b2+…+anbn=1=b1+b2+…bn,于是由①得
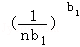
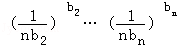 ≤1,即
≤1,即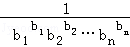 ≤nb1+b2+…bn=n,
≤nb1+b2+…bn=n,∴
 ≤
≤
 …
…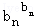 ,
,②再证

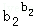 …
…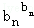 ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,记s=b12+b22+…+bn2.令ak=
 (k=1,2…,n),
(k=1,2…,n),则a1b1+a2b2+…+anbn=
 (b12+b22+…+bn2)=1=b1+b2+…bn,
(b12+b22+…+bn2)=1=b1+b2+…bn,于是由(1)得
 ≤1,
≤1,即
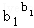
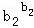 …
… ≤sb1+b2+…bn=s,
≤sb1+b2+…bn=s,∴
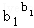
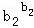 …
… ≤b12+b22+…+bn2,
≤b12+b22+…+bn2,综合①②,②得证.

练习册系列答案
相关题目
 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件: ,总有
,总有 ;(2)
;(2) ;(3) 若
;(3) 若 ,
, ,且
,且 ,则有
,则有 成立,则称
成立,则称 的值;
的值;  在区间
在区间 ,使得
,使得 且
且 , 求证:
, 求证: .
. .
. ,
, 时,若不等式
时,若不等式 恒成立,求
恒成立,求 的范围;
的范围; 在
在 内零点的个数,并说明理由.
内零点的个数,并说明理由. 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从 作
作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
, ,记点
,记点 ,点
,点 .如果
.如果 的取值范围是( )
的取值范围是( )



 ]=[x]
]=[x]
 的函数
的函数 (
( )有两个单调区间,则实数
)有两个单调区间,则实数 ,
, ,
, 满足( )
满足( ) 且
且


 是定义在
是定义在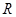 上的函数,且对任意实数
上的函数,且对任意实数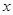 ,都有
,都有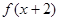 ≤
≤ ,
,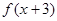 ≥
≥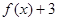 ,且
,且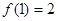 ,
,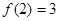 ,则
,则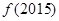 的值是
的值是