题目内容
某大学对该校参加某项活动的志愿者实施“社会教育实施”学分考核,该大学考核只有合格和优秀两个等次.若某志愿者考核为合格,授予 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中,甲、乙、丙三名志愿者所得学分之和为随机变量 ,求随机变量
,求随机变量 的
的
分布列和数学期望.
 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立.(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中,甲、乙、丙三名志愿者所得学分之和为随机变量
 ,求随机变量
,求随机变量 的
的分布列和数学期望.
(1)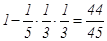 ;(2)
;(2) 的分布列为
的分布列为
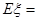
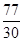
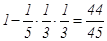 ;(2)
;(2) 的分布列为
的分布列为 | 1.5 | 2 | 2.5 | 3 |
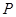 | 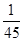 | 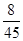 | 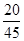 | 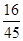 |
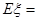
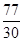
本试题主要考查了概率的求解,以及分布列和数学期望值的运算,理解题意,并能结合独立事件的概率公式进行求解。
解:(1)设丙考核优秀的概率为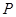 ,
,
依甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .
.
可得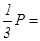
 ,即
,即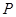 =
= .-----------------------------------------------(2分)
.-----------------------------------------------(2分)
于是,甲、乙、丙三人中至少有一名考核为优秀的概率为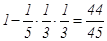 .----(4分)
.----(4分)
(2)依题意
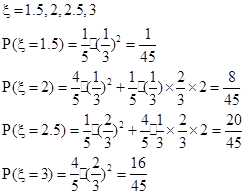
-----------------(4分)
于是 的分布列为
的分布列为
故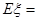
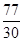 -----------------------(2分)
-----------------------(2分)
解:(1)设丙考核优秀的概率为
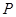 ,
,依甲、乙考核为优秀的概率分别为
 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .
.可得
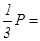
 ,即
,即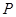 =
= .-----------------------------------------------(2分)
.-----------------------------------------------(2分)于是,甲、乙、丙三人中至少有一名考核为优秀的概率为
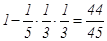 .----(4分)
.----(4分)(2)依题意
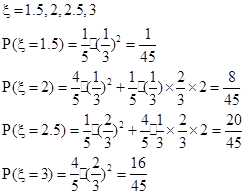
-----------------(4分)
于是
 的分布列为
的分布列为 | 1.5 | 2 | 2.5 | 3 |
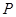 | 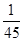 | 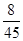 | 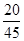 | 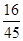 |
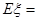
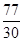 -----------------------(2分)
-----------------------(2分)
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
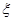 ,求
,求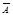 ,
,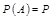 ,令随机变量
,令随机变量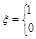
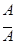 则
则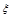 的方差为( )
的方差为( )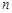 个红球(
个红球( 且
且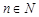 )和
)和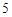 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。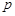 ;
;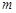 ,求
,求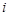 号的有
号的有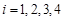 ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。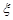 表示所取球的标号,求
表示所取球的标号,求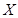 ,求
,求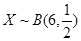 ,则
,则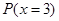 的值为
的值为



 ~
~ ,且
,且 ,
, ,则
,则 ▲ ,
▲ , ▲ .
▲ . ;
;
 表示出现正面向上的纪念币的个数。
表示出现正面向上的纪念币的个数。 望;
望; 中,若
中,若 的值最大,求a的最大值。
的值最大,求a的最大值。 ,且只有
,且只有 发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
 )目标被击中的概率;
)目标被击中的概率;  .
.