题目内容
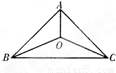
 三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且AB=AC=20
三个城市襄阳、荆州、武汉分别位于A,B,C三点处(如右图),且AB=AC=20| 2 |
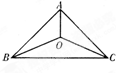
(Ⅰ)设OB=x(km),将y表示为x的函数;
(Ⅱ)由(Ⅰ)中建立的函数关系,确定货运中转站的位置,使修建的道路的总长度最短.
分析:(Ⅰ)设OB=xkm,延长AO交BC于D,由题意知BD=DC=
BC=20,OB=OC,OA=AD-OD=
-OD=20-OD,由此能够将y表示为x的函数.
(Ⅱ)由y=2x+20-
,知y′=2-
,由此能推导出当货物中转站建立在三角形区域内,且到B,C两点的距离均为
km时,修建的道路和总长度最短.
| 1 |
| 2 |
| AC2-DC2 |
(Ⅱ)由y=2x+20-
| x2-202 |
| x | ||
|
40
| ||
| 3 |
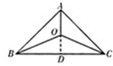
解答:解:(Ⅰ)设OB=x(km),延长AO交BC于D,
由题意知BD=DC=
BC=20,OB=OC,
OA=AD-OD=
-OD=20-OD,
在Rt△ODB中,OD=
=
,
∴y=OA+OB+OC=2x+20-
,20≤x≤20
.
(Ⅱ)∵y=2x+20-
,
∴y′=2-
,
∵20≤x≤20
,
∴x∈[20,
)时,y′0.
∴函数在x=
时,取得极小值,这个极小值是函数在[20,20
]上的最小值.
所以,当货物中转站建立在三角形区域内,且到B,C两点的距离均为
km时,修建的道路和总长度最短.
由题意知BD=DC=
| 1 |
| 2 |
OA=AD-OD=
| AC2-DC2 |
在Rt△ODB中,OD=
| OB2-DB2 |
| x2-202 |
∴y=OA+OB+OC=2x+20-
| x2-202 |
| 2 |
(Ⅱ)∵y=2x+20-
| x2-202 |
∴y′=2-
| x | ||
|
∵20≤x≤20
| 2 |
∴x∈[20,
40
| ||
| 3 |
∴函数在x=
40
| ||
| 3 |
| 2 |

所以,当货物中转站建立在三角形区域内,且到B,C两点的距离均为
40
| ||
| 3 |
点评:本题考查导数在求最大值和求最小值中的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
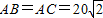 km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.
km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.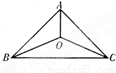
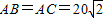 km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.
km,BC=40km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与B、C等距离的O点处,并修建道路OA,OB,OC.记修建的道路的总长度为ykm.