题目内容
定义函数
,若存在常数C，对于任意的
，存在唯一的
，使得
，则称函数
在D上的“均值”为
，已知
，则函数
上的均值为（ ）
A． | B． | C． | D．10 |
A
解析试题分析：因为过点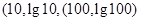
的中点的纵坐标为
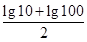，所以对于任意的，存在唯一的，使得
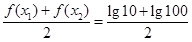.所以均值
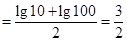.故选A.本小题的关键是考查函数的对称性问题.
考点：1.新定义的函数问题.2.函数的对称性.
练习册系列答案
相关题目
已知
是方程
的两根，且
，
,
，求
的最大值与最小值之和为( )．
| A．2 | B． | C． | D．1 |
设
，
，
，则
的大小顺序为（ ）
A． | B． | C． | D． |
函数
的零点所在区间是（ ）
A． | B． | C． | D． |
对
、
，运算“
”、“
”定义为：
=
，
=
，则下列各式其中不恒成立的是（ ）
⑴
⑵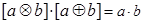
⑶
⑷
| A．⑴、⑶ | B．⑵、⑷ |
| C．⑴、⑵、⑶ | D．⑴、⑵、⑶、⑷ |
如果二次函数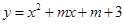
不存在零点，则
的取值范围是（ ）
A． | B． |
C． | D． |
在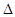
ABC中，若
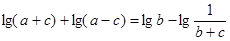，则A=（ ）
A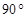． | B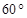． | C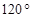． | D． |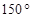
设
，则
（ ）
A． | B．0 | C． | D． |
已知函数f(x)＝
则f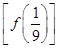
的值是( )
| A．4 | B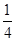． | C．－4 | D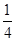．－ |