题目内容
已知:函数f(x)是定义在[-1,0)∪(0,1]上的偶函数,当x∈[-1,0)时,f(x)=x3-ax(a为实数).
(1)当x∈(0,1]时,求f(x)的解析式;
(2)若a>3,试判断f(x)在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值1?若存在,求出a的值;若不存在,请说明理由.
解:(1)设x∈(0,1],则-x∈[-1,0),∴f(-x)=-x3+ax
又∵f(x)是偶函数,f(-x)=f(x)
∴f(x)=-x3+ax,x∈(0,1]
(2)f′(x)=-3x2+a,
∵x∈(0,1]∴-3x2∈[-3,0),
又∵a>3∴a-3x2>0即f′(x)>0
∴f(x)在(0,1]上为增函数.
(3)当a>3时,f(x)在(0,1]上是增函数,
∴fmax=f(1)=a-1=1∴a=2,(不合题意,舍去)
当0≤a≤3时,f′(x)=a-3x2,令f′(x)=0,∴x= 如下表:
如下表:
∴f(x)在x= 处取得最大值-
处取得最大值-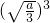 +a
+a =1
=1
∴a=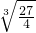 <3∴x=
<3∴x= <1,满足条件
<1,满足条件
当a<0时,f′(x)=a-3x2<0
f(x)在(0,1]上单调递减,f(x)在(0,1]无最大值.
∴存在a=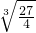 ,使f(x)在(0,1]上有最大值1.
,使f(x)在(0,1]上有最大值1.
分析:(1)当x∈(0,1]时,求f(x)的解析式;求哪段上的函数解析式,就在哪个区间上任意取x,则-x在对称的区间上,根据对称区间上的解析式及奇偶性求得.
(2)若a>3,试判断f(x)在(0,1]上的单调性,并证明你的结论;三次函数判断单调性可利用其导函数在(0,1)上的对应值的正负来判断.
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值1?若存在,求出a的值;若不存在,请说明理由,分析f′(x)=-3x2+a由x∈(0,1]∴-3x2∈[-3,0),故根据f′(x)的正负可将a分为a>3,0<a<3,a<0三种情况分类讨论即可.
点评:本题考查了三次函数的单调性问题,需要借助导数来研究.要注意前一问往往为后一问提供解题思路,在第3问中分类是解决问题的难点和关键.
又∵f(x)是偶函数,f(-x)=f(x)
∴f(x)=-x3+ax,x∈(0,1]
(2)f′(x)=-3x2+a,
∵x∈(0,1]∴-3x2∈[-3,0),
又∵a>3∴a-3x2>0即f′(x)>0
∴f(x)在(0,1]上为增函数.
(3)当a>3时,f(x)在(0,1]上是增函数,
∴fmax=f(1)=a-1=1∴a=2,(不合题意,舍去)
当0≤a≤3时,f′(x)=a-3x2,令f′(x)=0,∴x=
 如下表:
如下表:| x | (0, ) ) |  | ( ,1) ,1) |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 最大值 | ↘ |
 处取得最大值-
处取得最大值-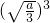 +a
+a =1
=1 ∴a=
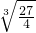 <3∴x=
<3∴x= <1,满足条件
<1,满足条件当a<0时,f′(x)=a-3x2<0
f(x)在(0,1]上单调递减,f(x)在(0,1]无最大值.
∴存在a=
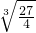 ,使f(x)在(0,1]上有最大值1.
,使f(x)在(0,1]上有最大值1.分析:(1)当x∈(0,1]时,求f(x)的解析式;求哪段上的函数解析式,就在哪个区间上任意取x,则-x在对称的区间上,根据对称区间上的解析式及奇偶性求得.
(2)若a>3,试判断f(x)在(0,1]上的单调性,并证明你的结论;三次函数判断单调性可利用其导函数在(0,1)上的对应值的正负来判断.
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值1?若存在,求出a的值;若不存在,请说明理由,分析f′(x)=-3x2+a由x∈(0,1]∴-3x2∈[-3,0),故根据f′(x)的正负可将a分为a>3,0<a<3,a<0三种情况分类讨论即可.
点评:本题考查了三次函数的单调性问题,需要借助导数来研究.要注意前一问往往为后一问提供解题思路,在第3问中分类是解决问题的难点和关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目