题目内容
设A={(x,y)|y=![]() ,a>0},B={(x,y)|(x–1)2+(y–
,a>0},B={(x,y)|(x–1)2+(y–![]() )2=a2,a>0},且A∩B≠
)2=a2,a>0},且A∩B≠![]() ,求a的最大值与最小值.
,求a的最大值与最小值.
amin=2![]() –2, amax=2
–2, amax=2![]() +2.
+2.
解析:
∵集合A中的元素构成的图形是以原点O为圆心,![]() a为半径的半圆;集合B中的元素是以点O′(1,
a为半径的半圆;集合B中的元素是以点O′(1,![]() )为圆心,a为半径的圆.如图所示:
)为圆心,a为半径的圆.如图所示:
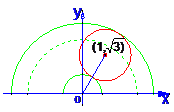
∵A∩B≠![]() ,∴半圆O和圆O′有公共点.
,∴半圆O和圆O′有公共点.
显然当半圆O和圆O′外切时,a最小
![]() a+a=|OO′|=2,∴amin=2
a+a=|OO′|=2,∴amin=2![]() –2
–2
当半圆O与圆O′内切时,半圆O的半径最大,即![]() a最大.
a最大.
此时![]() a–a=|OO′|=2,∴amax=2
a–a=|OO′|=2,∴amax=2![]() +2.
+2.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
设A={x|y=ln(2+x-x2),x∈R},B={y|y=
,x∈A},则CAB=( )
| x+2 |
| A、(-∞,-1]∪[2,+∞) |
| B、(-1,0) |
| C、(-∞,0]∪[2,+∞) |
| D、(-1,1] |