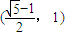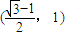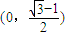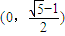题目内容
已知以椭圆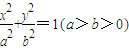 的右焦点F为圆心,a为半径的圆与直线l:
的右焦点F为圆心,a为半径的圆与直线l: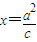 (其中
(其中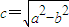 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )A.
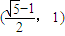
B.
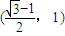
C.
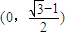
D.
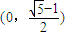
【答案】分析:根据a为半径的圆与椭圆的右准线交于不同的两点可知a大于焦准距即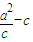 <a,不等式两边同时除以a,可得
<a,不等式两边同时除以a,可得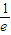 -e<1进而可得e的范围.又根据e<1,综合得e的范围.
-e<1进而可得e的范围.又根据e<1,综合得e的范围.
解答:解:∵a为半径的圆与椭圆的右准线交于不同的两点
∴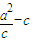 <a,
<a,
∴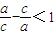 ,即
,即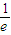 -e<1
-e<1
解得e>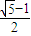
又因e<1,
∴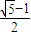 <e<1
<e<1
故选A
点评:本题主要考查椭圆的性质.属基础题.
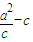 <a,不等式两边同时除以a,可得
<a,不等式两边同时除以a,可得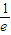 -e<1进而可得e的范围.又根据e<1,综合得e的范围.
-e<1进而可得e的范围.又根据e<1,综合得e的范围.解答:解:∵a为半径的圆与椭圆的右准线交于不同的两点
∴
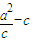 <a,
<a,∴
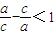 ,即
,即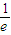 -e<1
-e<1解得e>
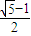
又因e<1,
∴
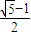 <e<1
<e<1故选A
点评:本题主要考查椭圆的性质.属基础题.

练习册系列答案
相关题目
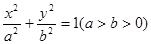 的右焦点F为圆心,
的右焦点F为圆心,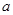 为半径的圆与直线
为半径的圆与直线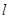 :
: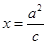 (其中
(其中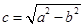 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )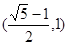 B.
B.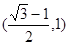 C.
C.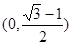 D.
D.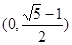
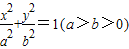 的右焦点F为圆心,a为半径的圆与直线l:
的右焦点F为圆心,a为半径的圆与直线l: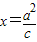 (其中
(其中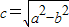 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )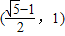
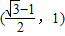
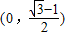
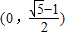
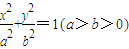 的右焦点F为圆心,a为半径的圆与直线l:
的右焦点F为圆心,a为半径的圆与直线l: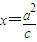 (其中
(其中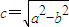 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )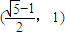
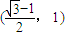
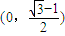
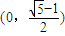
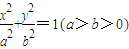 的右焦点F为圆心,a为半径的圆与直线l:
的右焦点F为圆心,a为半径的圆与直线l: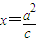 (其中
(其中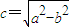 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )