题目内容
试根据复合函数的求导法则,研究函数f(x)=xx(x>0)的性质,并回答:下列命题中假命题的个数是( )①f(x)的极大值为1;
②f(x)的极小值为1;
③f(x)的一个单调递增区间是
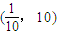 .
.A.0
B.1
C.2
D.3
【答案】分析:根据条件,对f(x)=xx=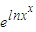 =exlnx,利用复合函数求导法则求出f′(x),令其等于0即可得到函数的单调区间与极值.
=exlnx,利用复合函数求导法则求出f′(x),令其等于0即可得到函数的单调区间与极值.
解答:解:∵f(x)=xx=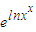 =exlnx,
=exlnx,
∴f′(x)=(xx)′=exlnx(lnx+1)=xx(lnx+1)=0
得x=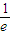

当x=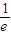 时,f(x)取极小值为
时,f(x)取极小值为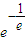 ,
,
f(x)的单调递增区间是(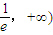 .
.
故命题①②③全错,
故选D.
点评:本题考查对数的恒等变形,以及复合函数求导法则,利用导数研究函数的单调性和极值问题,考查了运算能力和分析解决问题的能力,以及计算能力,属中档题.
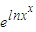 =exlnx,利用复合函数求导法则求出f′(x),令其等于0即可得到函数的单调区间与极值.
=exlnx,利用复合函数求导法则求出f′(x),令其等于0即可得到函数的单调区间与极值.解答:解:∵f(x)=xx=
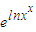 =exlnx,
=exlnx,∴f′(x)=(xx)′=exlnx(lnx+1)=xx(lnx+1)=0
得x=
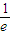

当x=
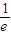 时,f(x)取极小值为
时,f(x)取极小值为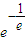 ,
,f(x)的单调递增区间是(
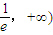 .
.故命题①②③全错,
故选D.
点评:本题考查对数的恒等变形,以及复合函数求导法则,利用导数研究函数的单调性和极值问题,考查了运算能力和分析解决问题的能力,以及计算能力,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
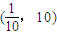 .
.