题目内容
设A、B是椭圆3x2+y2=λ上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点,
(Ⅰ)确定λ的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的λ,使得A、B、C、D四点在同一个圆上?并说明理由。
(Ⅰ)确定λ的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的λ,使得A、B、C、D四点在同一个圆上?并说明理由。
解:(Ⅰ)依题意,可设直线AB的方程为y=k(x-1),
代入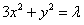 ,整理得
,整理得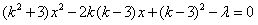 , ①
, ①
设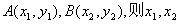 是方程①的两个不同的根,
是方程①的两个不同的根,
∴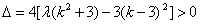 , ②
, ②
且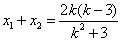 ,
,
由N(1,3)是线段AB的中点,得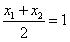 ,
,
∴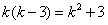 ,解得k=-1,
,解得k=-1,
代入②得,λ>12,
即λ的取值范围是(12,+∞),
于是,直线AB的方程为y-3=-(x-1),即x+y-4=0。
(Ⅱ)∵CD垂直平分AB,
∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得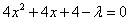 ,
,
又设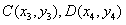 ,CD的中点为
,CD的中点为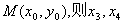 是方程③的两根,
是方程③的两根,
∴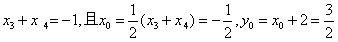 ,即
,即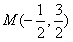 ,
,
于是由弦长公式可得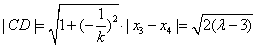 , ④
, ④
将直线AB的方程x+y-4=0,
代入椭圆方程得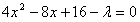 , ⑤
, ⑤
同理可得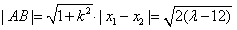 , ⑥
, ⑥
∵当λ>12时,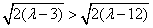 ,
,
∴|AB|<|CD|,
假设存在λ>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心,
点M到直线AB的距离为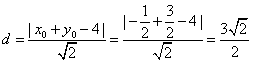 , ⑦
, ⑦
于是,由④、⑥、⑦式和勾股定理可得,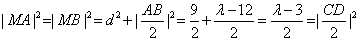 ,
,
故当λ>12时,A、B、C、D四点均在以M为圆心,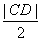 为半径的圆上。
为半径的圆上。

练习册系列答案
相关题目