题目内容
设A、B是椭圆3x2+y2=λ上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.(1)确定λ的取值范围,并求直线AB的方程;
(2)求以线段CD的中点M为圆心且与直线AB相切的圆的方程.
【答案】分析:(1)可设直线AB的方程为 y=k(x-1)+3,代入 椭圆3x2+y2=λ,可得 x1+x2=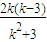 ,再由线段的中点公式求出 k=1,于是求得直线AB的方程.
,再由线段的中点公式求出 k=1,于是求得直线AB的方程.
(2)用点斜式求得直线CD的方程为 x-y+2=0,代入椭圆方程,整理得 4x2+4x+4-λ=0 ③,利用根与系数的关系和中点公式求得 M(- ,
, ),再求得M(-
),再求得M(- ,
, )到直线AB的距离 d,即可得到圆的标准方程.
)到直线AB的距离 d,即可得到圆的标准方程.
解答:解:(1)依题意,显然直线AB的斜率存在,可设直线AB的方程为 y=k(x-1)+3,
代入 椭圆3x2+y2=λ,整理得 (k2+3 ) x2-2k(k-3)x+(k-3)2-λ=0 ①
设 A ( x1,y1 ),B (x2,y2 ),则 x1,x2 是方程①的两个不同的根,
∴△=4k2 (k-3)2-4 (k2+3 )[(k-3)2-λ]>0 ②,且 x1+x2= .
.
由N(1,3)是线段AB的中点,得 =1,∴k(k-3)=k2+3,∴k=-1.
=1,∴k(k-3)=k2+3,∴k=-1.
代和②得 λ>12,即 λ 的取值范围是(12,+∞),于是直线AB的方程为 y-3=-(x-1),
即 x+y-4=0.
(2)∵CD垂直平分线段AB,∴直线CD的方程为 y-3=x-1,即 x-y+2=0,
代入椭圆方程,整理得 4x2+4x+4-λ=0 ③.
设 C(x3,y3 ),D (x4,y4 ),CD的中点为 M(x,y ),则 x3,x4 是方程③的两根,
∴x3+x4=-1,∴x=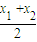 =-
=- ,y=x+1=
,y=x+1= ,即 M(-
,即 M(- ,
, ).
).
又 M(- ,
, )到直线AB的距离 d=
)到直线AB的距离 d=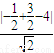 =
=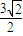 ,
,
故所求圆的方程为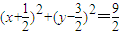 .
.
点评:本题考查直线和圆的位置关系,直线和圆锥曲线的位置关系,一元二次方程根与系数的关系,线段的中点公式的应用,求出点M的坐标是解题的难点.
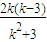 ,再由线段的中点公式求出 k=1,于是求得直线AB的方程.
,再由线段的中点公式求出 k=1,于是求得直线AB的方程.(2)用点斜式求得直线CD的方程为 x-y+2=0,代入椭圆方程,整理得 4x2+4x+4-λ=0 ③,利用根与系数的关系和中点公式求得 M(-
 ,
, ),再求得M(-
),再求得M(- ,
, )到直线AB的距离 d,即可得到圆的标准方程.
)到直线AB的距离 d,即可得到圆的标准方程.解答:解:(1)依题意,显然直线AB的斜率存在,可设直线AB的方程为 y=k(x-1)+3,
代入 椭圆3x2+y2=λ,整理得 (k2+3 ) x2-2k(k-3)x+(k-3)2-λ=0 ①
设 A ( x1,y1 ),B (x2,y2 ),则 x1,x2 是方程①的两个不同的根,
∴△=4k2 (k-3)2-4 (k2+3 )[(k-3)2-λ]>0 ②,且 x1+x2=
 .
.由N(1,3)是线段AB的中点,得
 =1,∴k(k-3)=k2+3,∴k=-1.
=1,∴k(k-3)=k2+3,∴k=-1.代和②得 λ>12,即 λ 的取值范围是(12,+∞),于是直线AB的方程为 y-3=-(x-1),
即 x+y-4=0.
(2)∵CD垂直平分线段AB,∴直线CD的方程为 y-3=x-1,即 x-y+2=0,
代入椭圆方程,整理得 4x2+4x+4-λ=0 ③.
设 C(x3,y3 ),D (x4,y4 ),CD的中点为 M(x,y ),则 x3,x4 是方程③的两根,
∴x3+x4=-1,∴x=
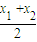 =-
=- ,y=x+1=
,y=x+1= ,即 M(-
,即 M(- ,
, ).
).又 M(-
 ,
, )到直线AB的距离 d=
)到直线AB的距离 d=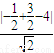 =
=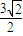 ,
,故所求圆的方程为
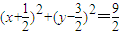 .
.点评:本题考查直线和圆的位置关系,直线和圆锥曲线的位置关系,一元二次方程根与系数的关系,线段的中点公式的应用,求出点M的坐标是解题的难点.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目