题目内容
已知:x>0,y>0,且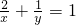 ,若x+2y>m2+2m恒成立,则实数m的取值范围是
,若x+2y>m2+2m恒成立,则实数m的取值范围是
- A.(-∞,-2]∪[4,+∞)
- B.(-∞,-4]∪[2,+∞)
- C.(-2,4)
- D.(-4,2)
D
分析:x+2y>m2+2m恒成立,即m2+2m<x+2y恒成立,只需求得x+2y的最小值即可.
解答:∵x>0,y>0,且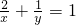 ,
,
∴x+2y=(x+2y)(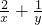 )=2+
)=2+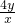 +
+ +2≥8(当且仅当x=4,y=2时取到等号).
+2≥8(当且仅当x=4,y=2时取到等号).
∴(x+2y)min=8.
∴x+2y>m2+2m恒成立,即m2+2m<(x+2y)min=8,
解得:-4<m<2.
故选D.
点评:本题考查基本不等式与函数恒成立问题,将问题转化为求x+2y的最小值是关键,考查学生分析转化与应用基本不等式的能力,属于中档题.
分析:x+2y>m2+2m恒成立,即m2+2m<x+2y恒成立,只需求得x+2y的最小值即可.
解答:∵x>0,y>0,且
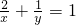 ,
,∴x+2y=(x+2y)(
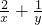 )=2+
)=2+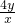 +
+ +2≥8(当且仅当x=4,y=2时取到等号).
+2≥8(当且仅当x=4,y=2时取到等号).∴(x+2y)min=8.
∴x+2y>m2+2m恒成立,即m2+2m<(x+2y)min=8,
解得:-4<m<2.
故选D.
点评:本题考查基本不等式与函数恒成立问题,将问题转化为求x+2y的最小值是关键,考查学生分析转化与应用基本不等式的能力,属于中档题.

练习册系列答案
相关题目