题目内容
已知椭圆C的对称轴为坐标轴,一个焦点为F(0,-
),点M(1,
)在椭圆C上
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线l:2x-y-2=0与椭圆C交于A,B两点,求△MAB的面积.
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线l:2x-y-2=0与椭圆C交于A,B两点,求△MAB的面积.
分析:(Ⅰ)由椭圆的定义求出长轴长,利用条件b2=a2-c2求出b,则椭圆C的方程可求;
(Ⅱ)联立直线和椭圆方程,解出交点,由点到直线距离公式求出三角形的高,则△MAB的面积可求.
(Ⅱ)联立直线和椭圆方程,解出交点,由点到直线距离公式求出三角形的高,则△MAB的面积可求.
解答:解:(Ⅰ)∵c=
,
∴2a=
+
=4,
∴a=2,b2=a2-c2=2,∴椭圆C的方程为
+
=1;
(Ⅱ)如图,
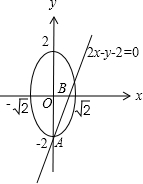
联立直线l与椭圆C的方程
.
解得
,
.
∴A(0,-2),B(
,
).
|AB|=
=
.
点M(1,
)到直线l的距离为d=
=
,
S△MAB=
|AB|•d=
×
×
=
.
| 2 |
∴2a=
(1-0)2+(
|
(1-0)2+(
|
∴a=2,b2=a2-c2=2,∴椭圆C的方程为
| y2 |
| 4 |
| x2 |
| 2 |
(Ⅱ)如图,
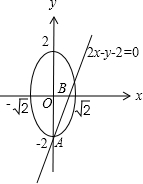
联立直线l与椭圆C的方程
|
解得
|
|
∴A(0,-2),B(
| 4 |
| 3 |
| 2 |
| 3 |
|AB|=
(
|
| 4 |
| 3 |
| 5 |
点M(1,
| 2 |
|2-
| ||
|
| ||
| 5 |
S△MAB=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
| ||
| 5 |
2
| ||
| 3 |
点评:本题考查阿勒椭圆的定义及简单几何性质,考查了直线与圆锥曲线的关系,训练了三角形面积的求法,是中档题.

练习册系列答案
相关题目
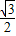 .
.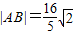 ,求直线l的方程.
,求直线l的方程.