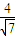题目内容
已知P是椭圆 上的一点,O是坐标原点,F是椭圆的左焦点且
上的一点,O是坐标原点,F是椭圆的左焦点且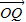 =
= (
( ),|
),| |=4,则点P到该椭圆左准线的距离为( )
|=4,则点P到该椭圆左准线的距离为( )A.6
B.4
C.3
D.

【答案】分析:由  =
= (
(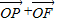 )可以推出Q是线段PF的中点,由P在椭圆上及
)可以推出Q是线段PF的中点,由P在椭圆上及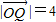 ,通过解方程组求得P点横坐标为
,通过解方程组求得P点横坐标为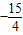 ,再求出到左准线的距离,即可得到答案.
,再求出到左准线的距离,即可得到答案.
解答:解:因为且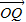 =
= (
(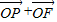 ),
),
所以∴Q是线段PF的中点,
∵由P在椭圆上且 ,设P(a,b),F(-4,0),Q(
,设P(a,b),F(-4,0),Q( ),
),
∴ ,∴
,∴ .
.
因为椭圆左准线x=-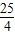 ,
,
所以点P到该椭圆左准线的距离 .
.
故选D.
点评:该题考查向量的线性表示以及椭圆的几何性质,另外还考查运算能力.是中档题.
 =
= (
(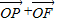 )可以推出Q是线段PF的中点,由P在椭圆上及
)可以推出Q是线段PF的中点,由P在椭圆上及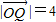 ,通过解方程组求得P点横坐标为
,通过解方程组求得P点横坐标为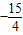 ,再求出到左准线的距离,即可得到答案.
,再求出到左准线的距离,即可得到答案.解答:解:因为且
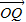 =
= (
(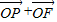 ),
),所以∴Q是线段PF的中点,
∵由P在椭圆上且
 ,设P(a,b),F(-4,0),Q(
,设P(a,b),F(-4,0),Q( ),
),∴
 ,∴
,∴ .
.因为椭圆左准线x=-
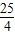 ,
,所以点P到该椭圆左准线的距离
 .
.故选D.
点评:该题考查向量的线性表示以及椭圆的几何性质,另外还考查运算能力.是中档题.

练习册系列答案
相关题目
 上的一点,
上的一点,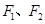 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若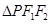 的内切圆的半径为
的内切圆的半径为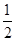 ,则
,则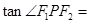 ( )
( ) B.
B. C.
C. D.
D.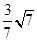
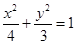 上的一点,
上的一点,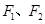 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若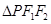 的内切圆的半径为
的内切圆的半径为 ,则
,则 ( )
( ) B.
B.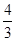 C.
C. D.
D.
 上的一点,则P到一条准线的距离与P到相应焦点的距离之比为( )
上的一点,则P到一条准线的距离与P到相应焦点的距离之比为( )