题目内容
已知集合P={x|x2-4x+3=0},集合Q={x|x2-ax+1=0},若P∪Q=P,求a的取值范围.
∵P={x|x2-4x+3=0}={x|x=1或x=3}={1,3}.
∵P∪Q=P,
∴Q⊆P,
若Q=∅,则△=a2-4<0,
即-2<a<2.
若Q≠∅,要使Q⊆P,
则Q={1}或{3}或{1,3},
若Q={1},
则
,即
,
∴a=2.
若Q={3},
则
,
即
,此时无解.
若Q={1,3},
则
,此时无解.
综上:-2<a≤2,
即a的取值范围是(-2,2].
∵P∪Q=P,
∴Q⊆P,
若Q=∅,则△=a2-4<0,
即-2<a<2.
若Q≠∅,要使Q⊆P,
则Q={1}或{3}或{1,3},
若Q={1},
则
|
|
∴a=2.
若Q={3},
则
|
即
|
若Q={1,3},
则
|
综上:-2<a≤2,
即a的取值范围是(-2,2].

练习册系列答案
相关题目
 ,函数
,函数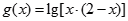 的定义域为
的定义域为 .
.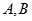 .
.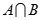 .
.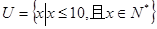 ,
,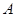

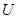 ,
,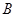
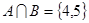 ,
, 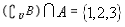 ,
,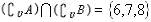 ,求集合
,求集合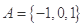 ,
,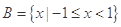 ,则
,则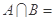
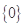
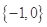
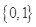
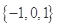
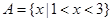 ,集合
,集合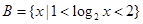 ,则
,则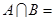 ( ).
( ).