题目内容
 如图,已知电路中4个开关闭合的概率都是
如图,已知电路中4个开关闭合的概率都是| 1 |
| 2 |
分析:灯泡不亮包括四个开关都开,或下边的2个都开,上边的2个中有一个开,这三种情况是互斥的,每一种情况中的事件是相互独立的,根据概率公式得到结果.
解答:解:由题意知,本题是一个相互独立事件同时发生的概率,
灯泡不亮包括四个开关都开,或下边的2个都开,上边的2个中有一个开,
这三种情况是互斥的,每一种情况中的事件是相互独立的,
∴灯泡不亮的概率是
×
×
×
+
×
×
×
+
×
×
×
=
,
∵灯亮和灯不亮是两个对立事件,
∴灯亮的概率是1-
=
,
故选 C.
灯泡不亮包括四个开关都开,或下边的2个都开,上边的2个中有一个开,
这三种情况是互斥的,每一种情况中的事件是相互独立的,
∴灯泡不亮的概率是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
∵灯亮和灯不亮是两个对立事件,
∴灯亮的概率是1-
| 3 |
| 16 |
| 13 |
| 16 |
故选 C.
点评:本题结合物理的电路考查了有关概率的知识,考查对立事件的概率和项和对立事件的概率,本题解题的关键是看出事件之间的关系,灯亮的情况比较多,需要从反面来考虑,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目

 且互相独立,灯亮的概率为 ( )。
且互相独立,灯亮的概率为 ( )。  B、
B、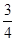 C、
C、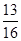 D、
D、

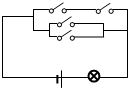 如图,已知电路中4个开关闭合的概率都是
如图,已知电路中4个开关闭合的概率都是 且互相独立,灯亮的概率为
且互相独立,灯亮的概率为


