题目内容
(1)求圆心在直线2x+y=0上,且与直线x+y-1=0相切于点P(2,-1)的圆的方程.
(2)求与圆(x-1)2+(y-2)2=5外切于(2,4)点且半径为2
的圆的方程.
(2)求与圆(x-1)2+(y-2)2=5外切于(2,4)点且半径为2
| 5 |
分析:(1)根据题意,圆心在直线2x+y=0上,又在过点P(2,-1)且与直线x+y-1=0垂直的直线x-y-3=0上,解方程组求得圆心C的坐标,可得半径r=|CP|的值,
从而得到所求圆的方程.
(2)根据两个圆的圆心连心线经过切点和原点,设所求圆心M(a,b),则由 KOM=KOC=2=
、b>0 以及|CM|=3
=
,求得a、b的值,
可得所求的圆的方程.
从而得到所求圆的方程.
(2)根据两个圆的圆心连心线经过切点和原点,设所求圆心M(a,b),则由 KOM=KOC=2=
| b |
| a |
| 5 |
| (a-1)2+(b-2)2 |
可得所求的圆的方程.
解答:解:(1)根据题意,圆心在过点P(2,-1)且与直线x+y-1=0垂直的直线为x-y-3=0,…(2分)
由
,求得
,即圆心C(1,-2),半径r=|CP|=
,…(4分)
所求圆的方程为 (x-1)2+(y+2)2=2. …(6分)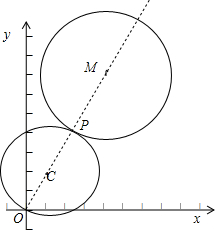
(2)两个圆的圆心连心线斜率k=
=2=KOC,
设所求圆心M(a,b),…(8分)
由题意可得 KOM=KOC=2=
①,
且b>0 ②,
且|CM|=3
=
③.
由①②③可得 a=4、b=8,…(10分)
∴所求的圆的方程为 (x-4)2+(y-8)2=20. …(12分)
由
|
|
| 2 |
所求圆的方程为 (x-1)2+(y+2)2=2. …(6分)

(2)两个圆的圆心连心线斜率k=
| 4-2 |
| 2-1 |
设所求圆心M(a,b),…(8分)
由题意可得 KOM=KOC=2=
| b |
| a |
且b>0 ②,
且|CM|=3
| 5 |
| (a-1)2+(b-2)2 |
由①②③可得 a=4、b=8,…(10分)
∴所求的圆的方程为 (x-4)2+(y-8)2=20. …(12分)
点评:本题主要考查求圆的标准方程,直线和圆、圆和圆的位置关系的应用,属于中档题.

练习册系列答案
相关题目
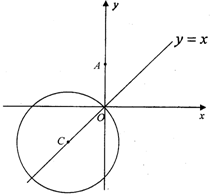 如图,已知圆C:x2+y2+10x+10y=0,点A(0,6).
如图,已知圆C:x2+y2+10x+10y=0,点A(0,6).