题目内容
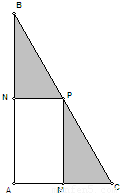
世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].(1)试用x表示S,并求S的取值范围;
(2)设矩形AMPN健身场地每平方米的造价为
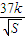 ,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为
,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为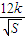 (k为正常数),求总造价T关于S的函数T=f(S);试问如何选取|AM|的长使总造价T最低(不要求求出最低造价).
(k为正常数),求总造价T关于S的函数T=f(S);试问如何选取|AM|的长使总造价T最低(不要求求出最低造价).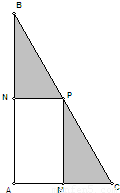
【答案】分析:(1)根据题意,分析可得,欲求健身场地占地面积,只须求出图中矩形的面积即可,再结合矩形的面积计算公式求出它们的面积即得,最后再根据二次函数的性质得出其范围;
(2)对于(1)所列不等式,考虑到其中两项之积为定值,可利用基本不等式求它的最大值,从而解决问题.
解答:解:(1)在Rt△PMC中,显然|MC|=30-x,∠PCM=60°
∴|PM|=|MC|tan∠PCM=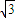 (30-x),…2分
(30-x),…2分
矩形AMPN的面积S=|PM||MC|= x(30-x),x∈[10,20]…4分
x(30-x),x∈[10,20]…4分
于是200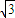 ≤S≤225
≤S≤225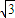 为所求.…6分
为所求.…6分
(2)矩形AMPN健身场地造价T1=37k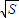 …7分
…7分
又△ABC的面积为450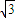 ,即草坪造价T2=
,即草坪造价T2=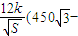 S)…8分
S)…8分
由总造价T=T1+T2,∴T=25k(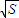 +
+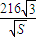 ),200
),200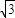 ≤S≤225
≤S≤225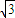 .…10分
.…10分
∴T=25k(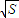 +
+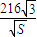 ),200
),200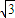 ≤S≤225
≤S≤225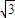
∵ +
+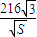 ≥12
≥12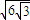 ,…11分
,…11分
当且仅当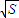 =
=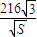 即S=216
即S=216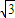 时等号成立,…12分
时等号成立,…12分
此时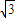 x(30-x)=216
x(30-x)=216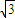 ,解得x=12或x=18,
,解得x=12或x=18,
所以选取|AM|的长为12米或18米时总造价T最低.…14分.
点评:本小题主要考查函数模型的选择与应用、基本不等式的应用、矩形的面积等基础知识,属于基础题.
(2)对于(1)所列不等式,考虑到其中两项之积为定值,可利用基本不等式求它的最大值,从而解决问题.
解答:解:(1)在Rt△PMC中,显然|MC|=30-x,∠PCM=60°
∴|PM|=|MC|tan∠PCM=
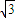 (30-x),…2分
(30-x),…2分矩形AMPN的面积S=|PM||MC|=
 x(30-x),x∈[10,20]…4分
x(30-x),x∈[10,20]…4分于是200
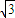 ≤S≤225
≤S≤225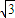 为所求.…6分
为所求.…6分(2)矩形AMPN健身场地造价T1=37k
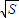 …7分
…7分又△ABC的面积为450
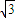 ,即草坪造价T2=
,即草坪造价T2=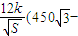 S)…8分
S)…8分由总造价T=T1+T2,∴T=25k(
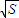 +
+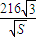 ),200
),200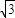 ≤S≤225
≤S≤225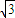 .…10分
.…10分∴T=25k(
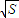 +
+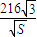 ),200
),200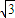 ≤S≤225
≤S≤225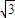
∵
 +
+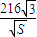 ≥12
≥12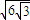 ,…11分
,…11分当且仅当
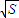 =
=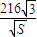 即S=216
即S=216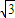 时等号成立,…12分
时等号成立,…12分此时
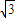 x(30-x)=216
x(30-x)=216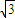 ,解得x=12或x=18,
,解得x=12或x=18,所以选取|AM|的长为12米或18米时总造价T最低.…14分.
点评:本小题主要考查函数模型的选择与应用、基本不等式的应用、矩形的面积等基础知识,属于基础题.

练习册系列答案
相关题目
 (2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].
(2012•浦东新区一模)世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地,如图点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x,x∈[10,20].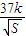 ,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为
,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为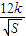 (k为正常数),求总造价T关于S的函数T=f(S);试问如何选取|AM|的长使总造价T最低(不要求求出最低造价).
(k为正常数),求总造价T关于S的函数T=f(S);试问如何选取|AM|的长使总造价T最低(不要求求出最低造价).