题目内容
为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡).现有一个由36名游客组成的旅游团到上海参观旅游,其中| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量ξ,求ξ的分布列及数学期望Eξ.
分析:(Ⅰ)由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡.记出事件,表示出事件的概率,根据互斥事件的概率公式,得到结论.
(Ⅱ)在该团的境内游客中随机采访3名游客,其中持银卡人数为随机变量ξ,则得到ξ的可能取值,做出变量在不同取值时对应的概率,写出分布列和期望.
(Ⅱ)在该团的境内游客中随机采访3名游客,其中持银卡人数为随机变量ξ,则得到ξ的可能取值,做出变量在不同取值时对应的概率,写出分布列和期望.
解答:解:(Ⅰ)∵现有一个由36名游客组成的旅游团到上海参观旅游,
其中
是境外游客,其余是境内游客.
∴由题意得,境外游客有27人,
其中9人持金卡;境内游客有9人,其中6人持银卡.
设事件B为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件A1为“采访该团3人中,1人持金卡,0人持银卡”,
事件A2为“采访该团3人中,1人持金卡,1人持银卡”.
P(B)=P(A1)+P(A2)
+
=
+
=
所以,在该团中随机采访3人,
恰有1人持金卡且持银卡者少于2人的概率是
.
(Ⅱ)ξ的可能取值为0,1,2,3
P(ξ=0)=
=
;,P(ξ=1)=
=
.
P=(ξ=2)=
=
,P(ξ=3)=
=
,
所以ξ的分布列为
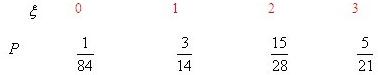
∴Eξ=0×
+1×
+2×
+3×
=2.
其中
| 3 |
| 4 |
∴由题意得,境外游客有27人,
其中9人持金卡;境内游客有9人,其中6人持银卡.
设事件B为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件A1为“采访该团3人中,1人持金卡,0人持银卡”,
事件A2为“采访该团3人中,1人持金卡,1人持银卡”.
P(B)=P(A1)+P(A2)
| ||||
|
| ||||||
|
=
| 9 |
| 34 |
| 27 |
| 170 |
=
| 36 |
| 85 |
所以,在该团中随机采访3人,
恰有1人持金卡且持银卡者少于2人的概率是
| 36 |
| 85 |
(Ⅱ)ξ的可能取值为0,1,2,3
P(ξ=0)=
| ||
|
| 1 |
| 84 |
| ||||
|
| 3 |
| 14 |
P=(ξ=2)=
| ||||
|
| 15 |
| 28 |
| ||
|
| 5 |
| 21 |
所以ξ的分布列为
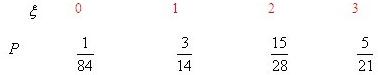
∴Eξ=0×
| 1 |
| 84 |
| 3 |
| 14 |
| 15 |
| 28 |
| 5 |
| 21 |
点评:考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
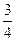 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有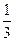 持金卡,在境内游客中有
持金卡,在境内游客中有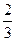 持银卡
持银卡 团的省内游客中随机采访3名
团的省内游客中随机采访3名 游客,设其中持银卡人数为随机变量
游客,设其中持银卡人数为随机变量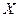 ,求
,求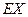
 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有 持金卡,在境内游客中有
持金卡,在境内游客中有 持银卡
持银卡 ,求
,求
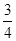 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有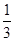 持金卡,在境内游客中有
持金卡,在境内游客中有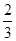 持银卡。.
持银卡。. 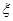 ,求
,求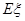 。
。