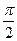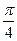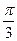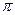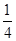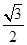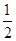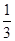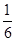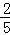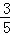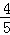题目内容
已知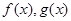 都是定义在R上的函数,
都是定义在R上的函数,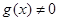 ,
,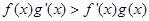 ,且
,且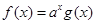 (
(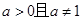 ),
), 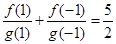 ,对于数列
,对于数列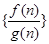 (n="1,2," ,10),任取正整数k(1≤k≤10),则其前k项和大于
(n="1,2," ,10),任取正整数k(1≤k≤10),则其前k项和大于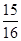 的概率是( ).
的概率是( ).
A.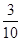 | B. | C.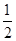 | D.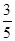 |
D
解析试题分析:由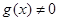 ,且
,且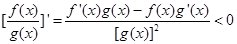 .所以函数
.所以函数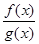 在R上递减.又由于
在R上递减.又由于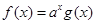 (
(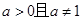 ).所以
).所以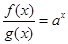 递减,即可得
递减,即可得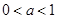 .由
.由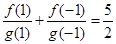 可得
可得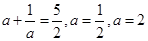 (舍去).所以
(舍去).所以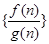 是一个首项为
是一个首项为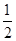 ,公比为
,公比为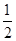 的等比数列,由等比数列求和公式即可得到当
的等比数列,由等比数列求和公式即可得到当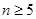 是符合条件即和大于
是符合条件即和大于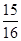 的概率为
的概率为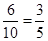 .故选D.
.故选D.
考点:1.函数导数的运算.2.数列的求和公式.3.概率问题.

练习册系列答案
相关题目
已知随机变量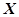 服从正态分布
服从正态分布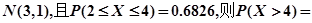 ( )
( )
A.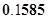 | B.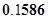 | C.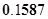 | D.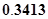 |
利用计算机产生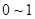 之间的均匀随机数
之间的均匀随机数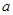 ,则事件“
,则事件“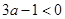 ”发生的概率为 ( )
”发生的概率为 ( )
A.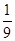 | B.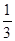 | C.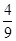 | D.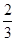 |
某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是( )
| A.0.8 | B.0.75 | C.0.6 | D.0.45 |
在区间[-3,3]上任取两数x,y,使 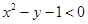 成立的概率为( )
成立的概率为( )
A.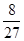 | B.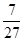 | C.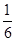 | D.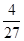 |