题目内容
6.已知f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个实数根,则t的取值范围为( )| A. | ($\frac{{e}^{2}+1}{e}$,+∞) | B. | (-∞,-$\frac{{e}^{2}+1}{e}$) | C. | (-$\frac{{e}^{2}+1}{e}$,-2) | D. | (2,$\frac{{e}^{2}+1}{e}$) |
分析 化简f(x)=|xex|=$\left\{\begin{array}{l}{x{e}^{x},x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,从而求导以确定函数的单调性,从而作出函数的简图,从而解得.
解答 解:f(x)=|xex|=$\left\{\begin{array}{l}{x{e}^{x},x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,
易知f(x)在[0,+∞)上是增函数,
当x∈(-∞,0)时,f(x)=-xex,
f′(x)=-ex(x+1),
故f(x)在(-∞,-1)上是增函数,在(-1,0)上是减函数;
作其图象如下,
且f(-1)=$\frac{1}{e}$;
故若方程f2(x)+tf(x)+1=0(t∈R)有四个实数根,
则方程x2+tx+1=0(t∈R)有两个不同的实根,且x1∈(0,$\frac{1}{e}$),x2∈($\frac{1}{e}$,+∞)∪{0},
故$\left\{\begin{array}{l}{0+0+1>0}\\{\frac{1}{{e}^{2}}+t\frac{1}{e}+1<0}\end{array}\right.$,或1=0
解得,t∈(-∞,-$\frac{{e}^{2}+1}{e}$),
故选:B.
点评 本题考查了分段函数的应用及导数的综合应用.

练习册系列答案
相关题目
1.过点(2,-1)作圆x2+y2=5的切线,其方程是( )
| A. | x-2y-4=0 | B. | 2x-y-5=0 | ||
| C. | 2x+y-3=0 | D. | 2x-y-5=0或x-2y+4=0 |
16.若a=2x,b=$\sqrt{x}$,c=log${\;}_{\frac{1}{2}}$x,则“x>1”是“a>b>c”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
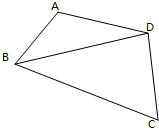 如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.
如图,在四边形ABCD中,BC=6,AD=CD=4,∠A+∠C=π,记△BCD,△ABD的面积分别为S1,S2,求S1-S2的最大值.