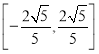题目内容
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”。在以下四个函数中:①
是“控制增长函数”。在以下四个函数中:①![]() ②
②![]() ③
③![]() ④
④![]() 是“控制增长函数”的有(空格上填入函数代码)________.
是“控制增长函数”的有(空格上填入函数代码)________.
【答案】②③④
【解析】
假设各函数为“控制增长函数”,根据定义推导f(x+a)≤f(x)+b恒成立的条件,判断a,b的存在性逐项判断即可得出答案.
对于①,f(x+a)≤f(x)+b可化为:(x+a)2+(x+a)+1≤x2+x+1+b,
即2ax≤﹣a2﹣a+b,即x![]() 对一切x∈R均成立,
对一切x∈R均成立,
由函数的定义域为R,故不存在满足条件的正常数a、b,故f(x)=x2+x+1不是“控制增长函数”;
对于②,若f(x)![]() 是“控制增长函数”,则f(x+a)≤f(x)+b可化为:
是“控制增长函数”,则f(x+a)≤f(x)+b可化为:![]() b,
b,
∴|x+a|≤|x|+b2+2b![]() 恒成立,又|x+a|≤|x|+a,
恒成立,又|x+a|≤|x|+a,
∴|x|+a≤|x|+b2+2b![]() ,∴
,∴![]() ,显然当a<b2时式子恒成立,
,显然当a<b2时式子恒成立,
∴f(x)![]() 是“控制增长函数”;
是“控制增长函数”;
对于③,∵﹣1≤f(x)=sin(x2)≤1,∴f(x+a)﹣f(x)≤2,
∴当b≥2时,a为任意正数,使f(x+a)≤f(x)+b恒成立,故f(x)=sin(x2)是“控制增长函数”;
对于④,若f(x)=xsinx是“控制增长函数”,则(x+a)sin(x+a)≤xsinx+b恒成立,
∵(x+a)sin(x+a)≤x+a,∴x+a≤xsinx+b≤x+b,即a≤b,
∴f(x)=xsinx是“控制增长函数”.
故答案为:②③④

练习册系列答案
相关题目