题目内容
已知三棱锥的顶点在底面内的射影为底面三角形的垂心,求证底面内任一顶点在其相对侧面内的射影也是此侧面三角形的垂心.
答案:
解析:
解析:
|
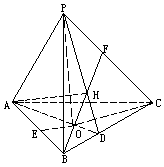
证明 如图,在三棱锥P-ABC中,P在底面内的射影O为△ABC的垂心,AO、CO分别交BC、AB于D、E.
由O为△ABC的垂心,知AO⊥BC. 由三垂线定理,可得BC⊥PA. 由BC⊥平面PAD,知BC⊥PD.
作AH⊥PD于H,则AH⊥平面PBC,即H为A在平面PBC内的射影. 由AH⊥平面PBC, 由三垂线定理,可知PC⊥AB,AB∩AH=A, 故PC⊥平面ABH,BH 由PH⊥BC,BH⊥PC,知H为△PBC的垂心. 同理可证B、C在其相对侧面内的射影也是侧面三角形PAC、PAB的垂心. 注意,复习、巩固上一单元的基础知识,也是学习本单元的目的之一. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
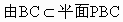 ,知平面PAD⊥平面PBC,PD为两平面交线.
,知平面PAD⊥平面PBC,PD为两平面交线.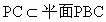 ,知AH⊥PC.
,知AH⊥PC.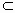 平面ABH.所以PC⊥BH,
平面ABH.所以PC⊥BH,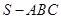 的各顶点都在一个半径为
的各顶点都在一个半径为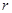 的球面上, 球心
的球面上, 球心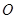 在
在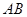 上,
上,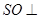 底面
底面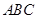 ,
,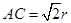 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )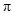 B.
B.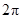 C.
C.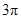 D.
D.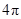
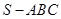 的各顶点都在一个半径为
的各顶点都在一个半径为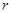 的球面上,球心
的球面上,球心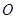 在
在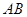 上,
上,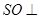 底面
底面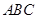 ,
,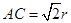 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )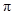 B.
B.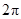 C.
C.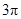 D.
D.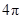
 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面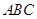 ,
, ,则三棱锥的体积与球的体积之比是 .
,则三棱锥的体积与球的体积之比是 .