题目内容
(1)求值:
+(
)-
+
-lg
+810.5log35+lg25+lg4
(2)解不等式:(log2x)2-4log4x-3>0.
| 1 | ||
|
| 1 |
| 27 |
| 1 |
| 3 |
| (lg3)2-lg9+1 |
| 1 |
| 3 |
(2)解不等式:(log2x)2-4log4x-3>0.
分析:(1)利用指数和对数的运算性质和运算法则,把
+(
)-
+
-lg
+810.5log35+lg25+lg4等价转化为2+3+
+lg3+3log325+2(lg5+lg2),由此能求出结果.
(2)利用对数的运算性质和运算法则,把(log2x)2-4log4x-3>0等价转化为(log2x)2-2log2x-3>0,再由换元法能够求出原不等式的解集.
| 1 | ||
|
| 1 |
| 27 |
| 1 |
| 3 |
| (lg3)2-lg9+1 |
| 1 |
| 3 |
| (lg3-1)2 |
(2)利用对数的运算性质和运算法则,把(log2x)2-4log4x-3>0等价转化为(log2x)2-2log2x-3>0,再由换元法能够求出原不等式的解集.
解答:解:(1)
+(
)-
+
-lg
+810.5log35+lg25+lg4
=2+3+
+lg3+3log325+2(lg5+lg2)
=5+1-lg3+lg3+25+2
=33.
(2)∵(log2x)2-4log4x-3>0,
∴(log2x)2-2log2x-3>0,
令t=log2x,得t2-2t-3>0,
∴t>3,或t<-1,
∴log2x>3,或log2x<-1,
∴x>8或0<x<
,
∴原不等式的解集为{x|x>8,或0<x<
}.
| 1 | ||
|
| 1 |
| 27 |
| 1 |
| 3 |
| (lg3)2-lg9+1 |
| 1 |
| 3 |
=2+3+
| (lg3-1)2 |
=5+1-lg3+lg3+25+2
=33.
(2)∵(log2x)2-4log4x-3>0,
∴(log2x)2-2log2x-3>0,
令t=log2x,得t2-2t-3>0,
∴t>3,或t<-1,
∴log2x>3,或log2x<-1,
∴x>8或0<x<
| 1 |
| 2 |
∴原不等式的解集为{x|x>8,或0<x<
| 1 |
| 2 |
点评:本题考查指数和对数的性质和运算法则的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
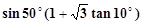 .
.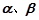 都是锐角,且
都是锐角,且 .
.