题目内容
若对定义在R上的可导函数f(x),恒有(4-x)f(2x)+2xf′(2x)>0,(其中f′(2x)表示函数f(x)的导函数f′(x)在2x的值),则f(x)( )
分析:根据条件构造函数g(x)=
,利用导数研究函数g(x)的单调性和极值,进而可以判断函数f(x)的取值情况.
| x4f(2x) |
| ex |
解答:解:函数g(x)=
,
则g′(x)=
=
=
=
,
∵(4-x)f(2x)+2xf′(2x)>0恒成立,
∴当x>0时,g'(x)>0,此时函数g(x)单调递增,
当x<0时,g'(x)<0,此时函数g(x)单调递减,
∴当x=0时,g(x)取得极小值,同时也是最小值g(0)=0,
∴g(x)=
≥g(0),
即g(x)=
≥0,当x≠0时,g(x)>0,
∴当x≠0时,f(x)>0,
∵(4-x)f(2x)+2xf′(2x)>0恒成立,
∴当x=0时,4f(0)+0>0恒成立,
∴f(0)>0,
综上无论x取何值,恒有f(x)>0,
故选C.
| x4f(2x) |
| ex |
则g′(x)=
| [x4f(2x)]′ex-x4f(2x)?[ex]′ |
| [ex]2 |
| 4x3f(2x)+2x4f′(2x)-x4f(2x) |
| ex |
=
| (4x3-x4)f(2x)+2x4f′(2x) |
| ex |
| x3[(4-x)f(2x)+2f′(2x)] |
| ex |
∵(4-x)f(2x)+2xf′(2x)>0恒成立,
∴当x>0时,g'(x)>0,此时函数g(x)单调递增,
当x<0时,g'(x)<0,此时函数g(x)单调递减,
∴当x=0时,g(x)取得极小值,同时也是最小值g(0)=0,
∴g(x)=
| x4f(2x) |
| ex |
即g(x)=
| x4f(2x) |
| ex |
∴当x≠0时,f(x)>0,
∵(4-x)f(2x)+2xf′(2x)>0恒成立,
∴当x=0时,4f(0)+0>0恒成立,
∴f(0)>0,
综上无论x取何值,恒有f(x)>0,
故选C.
点评:本题主要考查函数值判断,利用条件构造函数g(x)=
是解决本题的关键,利用导数研究函数的单调性和极值,考查学生的观察能力,综合性较强,难度较大.
| x4f(2x) |
| ex |

练习册系列答案
相关题目
已知函数y=f(x)是定义在R上的可导函数,且对?x∈R不等式:f(x)+xf′(x)<0恒成立,若a=3?f(3),b=
?f(
),c=(-2)?f(-2),则a、b、c的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、c>b>a |
| B、c>a>b |
| C、a>b>c |
| D、a>c>b |
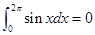 ;
;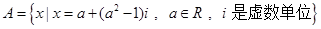 ,若
,若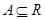 ,则
,则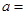 1
1 为定义在R上的可导函数,且
为定义在R上的可导函数,且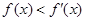 对于
对于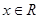 恒成立,则有
恒成立,则有 ,
, 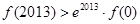 ;
;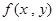 满足:(1)
满足:(1)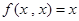 ,(2)
,(2)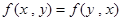 (3)
(3)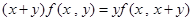 ,则
,则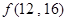 =
=
 ;
; ,若
,若 ,则
,则 1
1 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
; 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=