题目内容
已知函数![]() .
.![]()
(Ⅰ)若函数在区间![]() 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围;
(Ⅱ)如果当![]() 时,不等式
时,不等式![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(Ⅲ)求证![]() .
.
解析:(Ⅰ)因为![]()
![]() , x >0,则
, x >0,则![]() , (1分)
, (1分)
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在(0,1)上单调递增;在
在(0,1)上单调递增;在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 处取得极大值. (1分)
处取得极大值. (1分)
因为函数![]() 在区间
在区间![]() (其中
(其中![]() )上存在极值,
)上存在极值,
所以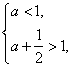 解得
解得![]() . (2分)
. (2分)
(Ⅱ)不等式![]() 即为
即为![]() 记
记![]()
所以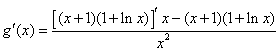
![]() (1分)
(1分)
令![]() ,则
,则![]() , (1分)
, (1分)
![]() ,
, ![]()
![]() 在
在![]() 上单调递增, (1分)
上单调递增, (1分)
![]() ,从而
,从而![]() ,
,
故![]() 在
在![]() 上也单调递增, (1分)
上也单调递增, (1分)
所以![]() ,所以
,所以![]() . (1分)
. (1分)
(Ⅲ)又(Ⅱ)知:![]() 恒成立,即
恒成立,即![]() , (1分)
, (1分)
令![]() ,则
,则![]() ,
,
所以 ![]() , (1分)
, (1分)
![]() ,
,
![]() ,
,
![]()
![]()
![]() , (1分)
, (1分)
叠加得:
![]()
![]() . (2分)
. (2分)
则![]() ,
,
![]() 所以
所以![]() . (1分)
. (1分)

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 ,
,
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求 ,
,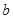 的值;
的值; ,
, 时,若函数
时,若函数 在区间[
在区间[ ,2]上的最大值为28,求
,2]上的最大值为28,求 ,
, 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点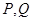 ,使得
,使得 是以
是以 (
( 轴上?请说明理由。
轴上?请说明理由。