题目内容
第29届奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是
.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率.
(Ⅲ)设随机变量X为在体操岗位服务的美国志愿者的个数,求X的分布列及期望.
| 3 |
| 5 |
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率.
(Ⅲ)设随机变量X为在体操岗位服务的美国志愿者的个数,求X的分布列及期望.
(Ⅰ)记至少一名美国志愿者被分到跳水岗位为事件A,
则A的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人x个,1≤x<6,
那么P(A)=1-
=
,
解得x=2,即来自美国的2人,来自英国的4人. (4分)
(Ⅱ)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是从6个人中选2个人,共有C62种结果,
满足条件的事件是从美国人中选一个,从英国人中选一个,共有C41C21种结果
记篮球岗位恰好美国人、英国人各有一人为事件E,那么P(E)=
=
,
所以篮球岗位恰好美国人、英国人各一人的概率是
. (8分)
(III)由题意知变量X的所有可能值为0,1,2,
根据变量对应的事件和等可能事件的概率公式得到,
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,
∴变量的分布列为:
(10分)
∴E(X)=0×
+1×
+2×
=
(人). (12分)
则A的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人x个,1≤x<6,
那么P(A)=1-
| ||||
|
| 3 |
| 5 |
解得x=2,即来自美国的2人,来自英国的4人. (4分)
(Ⅱ)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件是从6个人中选2个人,共有C62种结果,
满足条件的事件是从美国人中选一个,从英国人中选一个,共有C41C21种结果
记篮球岗位恰好美国人、英国人各有一人为事件E,那么P(E)=
| ||||
|
| 8 |
| 15 |
所以篮球岗位恰好美国人、英国人各一人的概率是
| 8 |
| 15 |
(III)由题意知变量X的所有可能值为0,1,2,
根据变量对应的事件和等可能事件的概率公式得到,
P(X=0)=
| ||||
|
| 2 |
| 5 |
| ||||||
|
| 8 |
| 15 |
| ||||
|
| 1 |
| 15 |
∴变量的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
∴E(X)=0×
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |

练习册系列答案
相关题目
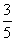 。
。