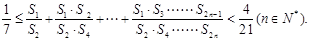题目内容
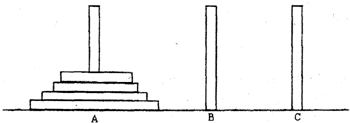
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(n∈N*)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A,B,C可供使用.
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1)写出a1,a2,a3,并求出an;
(2)记bn=an+1,求和
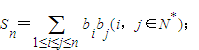 (其中
(其中 表示所有的积bibj(1≤i≤j≤n)的和)
表示所有的积bibj(1≤i≤j≤n)的和)(3)证明:
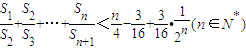 .
.
【答案】分析:(1)由题意要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,需要an-1次转移,然后将最大的那个圆盘转移到C柱上,需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,需要an-1次转移,所以有an=2an-1+1,利用构造法可求an;
(2)由第(1)问解答知bn=an+1=2n则 将bn代入利用等比数列求和公式求和即得;
将bn代入利用等比数列求和公式求和即得;
(3)由(2)求得和 ,利用利用放缩法结合等比数列求和可证.
,利用利用放缩法结合等比数列求和可证.
解答:解:(1)a1=1,a2=3,a3=7,
事实上,要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,
需要an-1次转移,然后将最大的那个圆盘转移到C柱上,
需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,
需要an-1次转移,所以有an=2an-1+1
则an+1=2(an-1+1)⇒an+1=2n,
所以an=2n-1
(2)由第(1)问解答知bn=an+1=2n
则
=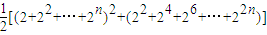
= =
=
(3)令 ,则由(2)得:
,则由(2)得:

所以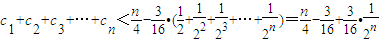 .
.
点评:本题的(1)问关键是从特殊中发现一般性的规律,考查构造法求数列的通项;(3)问体现等价转化的数学思想,同时应注意放缩法的运用.
(2)由第(1)问解答知bn=an+1=2n则
 将bn代入利用等比数列求和公式求和即得;
将bn代入利用等比数列求和公式求和即得;(3)由(2)求得和
 ,利用利用放缩法结合等比数列求和可证.
,利用利用放缩法结合等比数列求和可证.解答:解:(1)a1=1,a2=3,a3=7,
事实上,要将n个圆盘全部转移到C柱上,只需先将上面n-1个圆盘转移到B柱上,
需要an-1次转移,然后将最大的那个圆盘转移到C柱上,
需要一次转移,再将B柱上的n-1个圆盘转移到C柱上,
需要an-1次转移,所以有an=2an-1+1
则an+1=2(an-1+1)⇒an+1=2n,
所以an=2n-1
(2)由第(1)问解答知bn=an+1=2n
则

=
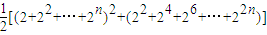
=
 =
=
(3)令
 ,则由(2)得:
,则由(2)得:
所以
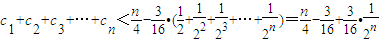 .
.点评:本题的(1)问关键是从特殊中发现一般性的规律,考查构造法求数列的通项;(3)问体现等价转化的数学思想,同时应注意放缩法的运用.

练习册系列答案
相关题目
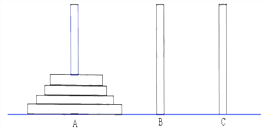 古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(n∈N*)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(n∈N*)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
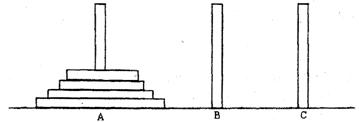
 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
 ,求和
,求和 (
( );
); 表示所有的积
表示所有的积 的和)
的和) .
.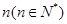 个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。
个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。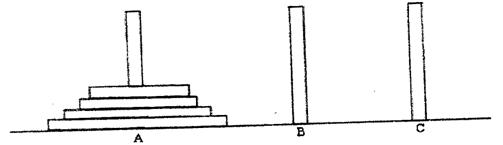
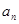 表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题:
表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题: ,并求出
,并求出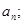
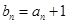 ,求和
,求和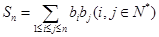 ;
;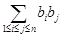 表示所有的积
表示所有的积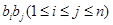 的和)
的和)