题目内容
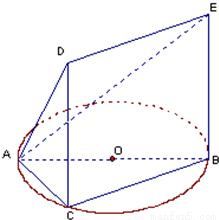
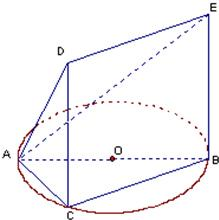
 如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
(1)证明:平面ACD⊥平面ADE;
(2)若AB=2,BC=1,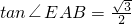 ,试求该几何体的体积V.
,试求该几何体的体积V.
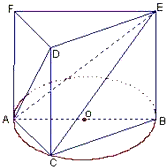 解:(1)证明:∵DC⊥平面ABC,BC?平面ABC,
解:(1)证明:∵DC⊥平面ABC,BC?平面ABC,∴DC⊥BC,
∵AB是圆O的直径,
∴BC⊥AC且DC∩AC=C,
∴BC⊥平面ADC,
∵四边形DCBE为平行四边形,
∴DE∥BC,
∴DE⊥平面ADC,
又∵DE?平面ADE,
∴平面ACD⊥平面ADE;
(2)所求简单组合体的体积:V=VE-ABC+VE-ADC
∵AB=2,BC=1,
 ,
,∴
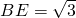 ,
,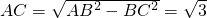 ,
,∴
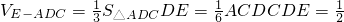
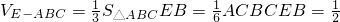
∴该简单几何体的体积V=1;
分析:(1)欲证平面ACD⊥平面ADE,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACD垂直,而根据BC⊥平面ADC,DE∥BC,可得DE⊥平面ADC;
(2)所求简单组合体的体积进行分解:V=VE-ABC+VE-ADC,然后利用体积公式进行求解,关键是几何体的高的求解.
点评:本小题主要考查空间中的线面关系,考查面面垂直的判定及简单组合体体积的计算,考查识图能力和逻辑思维能力,考查转化思想,属于基础题.

练习册系列答案
相关题目
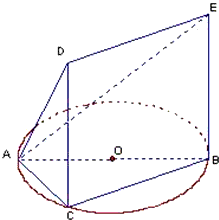
 如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
 ,试求该几何体的体积V.
,试求该几何体的体积V.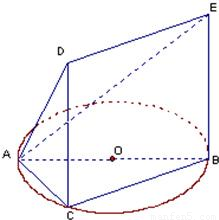
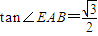 ,试求该几何体的体积V.
,试求该几何体的体积V.