题目内容
计算：1；1-4；1-4+9；1-4+9-16…各项的值，可以猜测：n∈N*，1-4+9-16+…+（-1）n+1n2=
1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
．分析：由1=1，1-4=-（1+2），1-4+9=1+2+3，1-4+9-16=-（1+2+3+4），…，中找出各式运算量之间的关系，归纳其中的规律，并大胆猜想，给出答案．
解答：解：∵1=1=（-1）1+1•1
1-4=-（1+2）=（-1）2+1•（1+2）
1-4+9=1+2+3=（-1）3+1•（1+2+3）
1-4+9-16=-（1+2+3+4）=（-1）4+1•（1+2+3+4）
…
所以猜想：1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
故答案为：1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
1-4=-（1+2）=（-1）2+1•（1+2）
1-4+9=1+2+3=（-1）3+1•（1+2+3）
1-4+9-16=-（1+2+3+4）=（-1）4+1•（1+2+3+4）
…
所以猜想：1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
故答案为：1-4+9-16+…+（-1）n+1•n2=（-1）n+1•（1+2+3+…+n）
点评：本题的考点是归纳推论，要求学生对给出的条件仔细观察找出规律，从而求解．归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
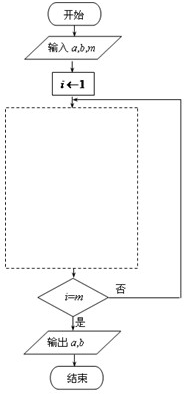若数列{an}，{bn}中，a1=a，b1=b，
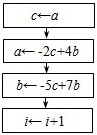B、
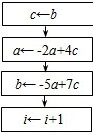
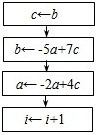D、
