题目内容
(坐标系与参数方程)求直线 (t为参数)被曲线
(t为参数)被曲线 所截的弦长.
所截的弦长.
【答案】分析:先将原极坐标方程曲线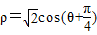 中的两边同乘以ρ后化成直角坐标方程,将直线l的参数方程化成普通方程,再利用直角坐标方程求出圆心到直线的距离,最后根据半径,圆心距,弦长的一半三者之间的关系即可求出弦长.
中的两边同乘以ρ后化成直角坐标方程,将直线l的参数方程化成普通方程,再利用直角坐标方程求出圆心到直线的距离,最后根据半径,圆心距,弦长的一半三者之间的关系即可求出弦长.
解答:解:将方程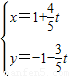 ,
,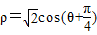 分别化为普通方程:3x+4y+1=0,x2+y2-x+y=0,…(5分)
分别化为普通方程:3x+4y+1=0,x2+y2-x+y=0,…(5分)
所以圆心坐标为:( ,-
,- ),半径为
),半径为 .
.
圆心到直线的距离为: =
= .
.
所以弦长=2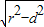 =2
=2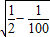 =
= …(10分)
…(10分)
点评:本题考查点的极坐标和直角坐标的互化、直线的参数方程,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
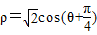 中的两边同乘以ρ后化成直角坐标方程,将直线l的参数方程化成普通方程,再利用直角坐标方程求出圆心到直线的距离,最后根据半径,圆心距,弦长的一半三者之间的关系即可求出弦长.
中的两边同乘以ρ后化成直角坐标方程,将直线l的参数方程化成普通方程,再利用直角坐标方程求出圆心到直线的距离,最后根据半径,圆心距,弦长的一半三者之间的关系即可求出弦长.解答:解:将方程
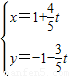 ,
,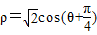 分别化为普通方程:3x+4y+1=0,x2+y2-x+y=0,…(5分)
分别化为普通方程:3x+4y+1=0,x2+y2-x+y=0,…(5分)所以圆心坐标为:(
 ,-
,- ),半径为
),半径为 .
.圆心到直线的距离为:
 =
= .
.所以弦长=2
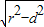 =2
=2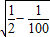 =
= …(10分)
…(10分)点评:本题考查点的极坐标和直角坐标的互化、直线的参数方程,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
相关题目
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)