题目内容
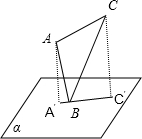
△ABC的顶点B在平面α内，A、C在α同侧，A′、C′是A、C的在平面α内的射影，且A′、C′、B三点共线，则平面ABC与平面α（ ）
分析：由题设知AA‘⊥α，CC’⊥α，AA‘BC’CC共面，由AA‘⊥α，AA’?△ABC，知△ABC⊥α．
解答：解：如图，∵△ABC的顶点B在平面α内，
A、C在α同侧，
A′、C′是A、C的在平面α内的射影，
∴AA‘⊥α，CC’⊥α，
∴AA‘C’C共面，
∵A′、C′、B三点共线，
∴AA‘BC’CC共面，
∵AA‘⊥α，AA’?△ABC，
∴△ABC⊥α．
故选B．
A、C在α同侧，
A′、C′是A、C的在平面α内的射影，
∴AA‘⊥α，CC’⊥α，
∴AA‘C’C共面，
∵A′、C′、B三点共线，
∴AA‘BC’CC共面，
∵AA‘⊥α，AA’?△ABC，
∴△ABC⊥α．
故选B．
点评：本题考查平面与平面的位置关系，是基础题．如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直．
练习册系列答案
相关题目
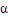上，已知它的底面边长为2，高h，边BC在平面上转动，若某个时刻它在平面
上的射影是等腰直角三角形，则h的取值范围是（ ）
]
]
]∪[
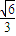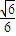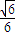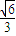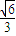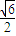，1]
]∪（
，1）