题目内容
已知点P为椭圆C: +
+ =1上动点,F1,F2分别是椭圆C的焦点,则|PF1|-|PF2|的最大值为
=1上动点,F1,F2分别是椭圆C的焦点,则|PF1|-|PF2|的最大值为
- A.2
- B.3
- C.2

- D.4
A
分析:根据椭圆的几何性质,可得当P与椭圆的右顶点重合时|PF1|的取得最大值且|PF2|取得最小值,故此时|PF1|-|PF2|取得最大值2,得到本题答案.
解答: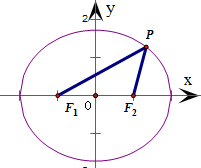 ∵点P为椭圆C:
∵点P为椭圆C: +
+ =1上动点,
=1上动点,
∴a=2,b= ,可得c=
,可得c= =1
=1
运动点P可得|PF1|∈[a-c,a+c],即|PF1|∈[1,3]
当P与椭圆的左顶点重合时,|PF1|的最小值为1;当P与椭圆的右顶点重合时,
|PF1|的最大值为3
同理,P与椭圆的左顶点重合时,|PF2|的最大值为3;当P与椭圆的右顶点重合时,|PF2|的最小值为1
∴当P与椭圆的右顶点重合时,|PF1|-|PF2|达到最大值,最大值为3-1=2.
故选:A
点评:本题给出椭圆上动点P,求它与左、右焦点距离之差的最大值,着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.
分析:根据椭圆的几何性质,可得当P与椭圆的右顶点重合时|PF1|的取得最大值且|PF2|取得最小值,故此时|PF1|-|PF2|取得最大值2,得到本题答案.
解答:
 ∵点P为椭圆C:
∵点P为椭圆C: +
+ =1上动点,
=1上动点,∴a=2,b=
 ,可得c=
,可得c= =1
=1运动点P可得|PF1|∈[a-c,a+c],即|PF1|∈[1,3]
当P与椭圆的左顶点重合时,|PF1|的最小值为1;当P与椭圆的右顶点重合时,
|PF1|的最大值为3
同理,P与椭圆的左顶点重合时,|PF2|的最大值为3;当P与椭圆的右顶点重合时,|PF2|的最小值为1
∴当P与椭圆的右顶点重合时,|PF1|-|PF2|达到最大值,最大值为3-1=2.
故选:A
点评:本题给出椭圆上动点P,求它与左、右焦点距离之差的最大值,着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
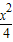 +
+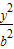 =1 (b>0)上的动点,且|OP|的最小值为1,其中O为坐标原点,则b= .
=1 (b>0)上的动点,且|OP|的最小值为1,其中O为坐标原点,则b= .